6.Ду с разделяющимися переменными.

Условие Эйлера всегда выполн. для ДУ вида М(х,у)dx + N(x,y)dy = 0 (1), где М(х,у) и N(x,y) – непрер. дифференцируемые ф-ции на некот. пром-ке. Общий интеграл этого ур-ия имеет вид: 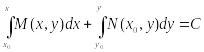(2), где (х,у)ϵD. В силу непрер. ф-ций М(х,у) и N(x,y) использ. ф-лы связи неопредел. и определ. интеграла, общий вид (1) можно записать так: (3). (1) – ур-ие с разделёнными переменными.

Часто ур-ия, для кот. усл. Эйлера не выполн. легко приводится к ур-ию в полных диф-лахпутём умножения ур-ия на спец. ф-цию наз. интегрируещим множителем. Его можно легко найти для ур-ия М(х,у)dx + N(x,y)dy = 0, если ф-ции М(х,у) и N(x,y) удовл. условию: и (4). (5). Домножим (5) на 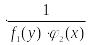. Ур-ие вида (5) наз. ур-ием с разделяющимися перемен. (6) – ур-ие с разделёнными переменными. Общий интеграл (6) имеет вид: .

Зам. ДУ (*) также наз. ур-ем с раздел. перемен. Это частный сл. ур-ия вида (5). ДУ м.б. привидено к виду (*). можно разл. след. сл.: 1) b=0, - это ур-ие разреш. непосредств. интегриров.; 2) а=0, - это частный сл. ур-ия с раздел. перемен.; 3) а∙b≠0, в этом сл. делается замена u=ax+by+c, где u – новая неизв. ф-ция. => и подставляем в ур-ие. Получ. ур-ие вида: 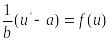- частный сл. ДУ с раздел. перемен.

7.Ду в полных дифференциалах.

Рассм. ур-ие вида М(х,у)dx + N(x,y)dy = 0 (1), где ф-ции М(х,у), N(x,y) – непрер. по обеим перем. в некот. связной обл. и одновременно не обращ. в 0, т.е. М²(х,у) + N²(x,y) 0.

Ур-ие (1) наз. ур-ие полных диф-лов, если его левая часть есть полный диф-л некот. ф-ции U(x,y), т.е. dU(x,y) = М(х,у)dx + N(x,y)dy. Тогда (1) можно записать в виде dU(x,y) = 0. И поэтому общий интегралл этого ур-ия имеет вид: U(x,y) = С.

Теор.(признак ур-ия полного диф-ла и построение его общего решения) Если ф-ции М(х,у) и N(x,y) – непрер. диф-мы в некотор. односвязной обл. D, тогда ДУ (1) будет ур-ием в полных диф-лах т. и т.т.к. выполн. условие для любого х,уϵD: (3) – условие Эйлера.

► =>) Пусть левая часть (1) явл. полным диф-лом некот. ф-ции U(x,y), а это значит dU = М(х,у)dx + N(x,y)dy. С другой стороны dU = . Отсюда имеют место тождества: и . Продиффер. эти равенства: и . Т.к. частные производные М(х,у) и N(x,y) непрер., то смешанные производные равны м/д собой, а значит мы получим условие (3).

<=) Пусть для М(х,у), N(x,y) выполн. усл. (3), покажим, что тогда Ǝ такая ф-ция U(x,y), что имеет место равенство dU(x,y) = М(х,у)dx + N(x,y)dy. Иначе говоря, ф-ция U(x,y) такая что: и (4). Пусть (.) (х₀, у₀) ϵD, где D – открытое односвязное мн-во, а поэтому (.) (х₀, у₀) ϵD вместе со своей некотор. окрестностью. Тогда из первого равенства (4): (5). Интегрирование имеет смысл т.к. D, где определена ф-ция М(х,у) односвязное мн-во. Отметим, что ϕ(у) – произв. ф-ция, дифференцируемая по у. Будем определять ϕ(у) таким обр., чтобы U(x,y) удовл. равенствам (4). Продифференцир. (5) по у: . В силу (3) имеем: , , , Подставим в (5) и получаем: U(x,y) = (6). Положим, что в (6) С=0 и возьмём одну из ф-ций U(x,y) при С=0 и тогда в силу (2) получим решение: . ◄

Зам. Как известно из курса мат. анализа ещё проще м.б. определить ф-цию U(x,y) по её полному диф-лу, взяв криволинейный интегралл от ф-ции М(х,у)dx + N(x,y)dy по контору м/д некотор. фиксир. (.)(х₀,у₀) и произв. (.)(х,у).