39.Понятие интеграла нормально с-мы. Первый интеграл нормальной с-мы. Общий интеграл.

Рассмотрим одно из равенств с-мы (12) ψ₁(х, у₁, ..., у_n) = C_i (13). Ф-ция ψ₁(х, у₁, ..., у_n) обращается в постоянную при замене у₁, ..., у_n любым частным решением с-мы (2), располож. в обл. задания общего решения (11). Т.е. имеем тождество: ψ₁(х, ϕ₁(х, С₁, ..., С_n), …, ϕ_n(х, С₁, ..., С_n)) C_i (14). Всякая ф-ция ψ₁(х, у₁, ..., у_n) обладающая таким св-вом наз. интегралом с-мы (2).

Опр. Ф-ция ψ₁(х, у₁, ..., у_n), не приводящаяся к постоянной наз. интегралом с-мы (2), если при замене у₁, ..., у_n любым частным решением этой с-мы, она обращается в постоянную.

Опр. Ф-ция ψ₁(х, у₁, ..., у_n), имеющая непрер. частные производные по (х, у₁, ..., у_n) и такая что, в рассматр. области частные произв. , , ..., не обращаются одновременно в 0 наз. интегралом с-мы (2), если полный дифференциал этой ф-ции обращается в 0 в силу с-мы (2), т.е. имеет место тождество: 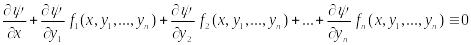(15).

Равенство ψ(х, у₁, ..., у_n) = С (16), где ψ(х, у₁, ..., у_n) – интеграл с-мы (2), а С – произвольная постоянная наз. первым интегралом с-мы (2).

Каждое равенство (12) явл. первым интегралом с-мы (2).

Совокупность первых интегралов обладает тем св-вом, что она разрешима относительно искомых ф-ций (х, у₁, ..., у_n). Причём в результате этого получаем общее решение (11) с-мы (2). Эту совокупность наз. общим интегралом с-мы (2) в обл. D.

40.Линейные с-мы ду. Линейно независимые с-мы функциональных векторов. Фундаментальная с-ма. Вронскиан.

Совокупность соотношений вида: (1), где у₁,у₂,...,у_n – искомые ф-ции от независим. перемен. х наз. с-мой обыкнов. ДУ 1-го порядка.

Будем предполагать ф-ции F₁,F₂,…,F_n такими, что с-ма (1) разрешима относит. производной от искомой ф-ции.

(2) – нормальная с-ма ДУ. Число ур-ий вход. в с-му (2) наз. порядком с-мы (2).

Если правые части (2) л.з. от искомых ф-ций у₁,у₂,...,у_n, т.е. с-ма (2) имеет вид: (3) – линейная с-ма ДУ, где р_kl(x) – заданные ф-ции, k={1,…,n},l={1,…,n}.

Если правые части (2) не зависят явно от х, т.е. (2) имеет вид: (4) – автономная, или стационарная с-ма ДУ.

у₁ = ϕ₁(х), у₂ = ϕ₂(х), ..., у_n = ϕ_n(х) (5) определ. и непрер. дифференц. в интервале [a,b] наз. решением с-мы (1) на [a,b], если оно обращает все ур-ия с-мы (1) в тождетсва.

Теор. Если ф-ции у₁(х), у₂(х), ..., у_m(x) л.з. на [a,b] и имеют производные до порядка (n-1) включительно, то определитель (х)ϵ[a,b] - определитель Вронского. Обознач. W(x) или W(у₁,у₂,..., у_m).

Теор. (критерий л.н. решений ЛОДУ). Для того чтобы решения у₁(х), у₂(х), ..., у_n(x) ЛОДУ L_n[y] = 0 с непрер. коэф. на [a,b] были л.н. на [a,b] Н. и Д., чтобы определитель Вронского W(x) ≠ 0 (х)ϵ[a,b].

► =>) Пусть ф-ции у₁(х), у₂(х), ..., у_n(x) л.н., это значит отпротивного W(x₀) = 0, х₀ ϵ[a,b]. Составим с-му n ур-ний: 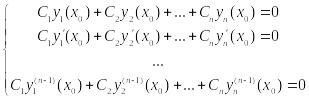(*). Определитель этой с-мы W(x₀) и т.к. W(x₀) = 0, то однородная с-ма линейных ур-ий имеет ненулевое решение С₁⁽⁰⁾, С₂⁽⁰⁾, ..., С_n⁽⁰⁾. Подставим это решение в с-му: 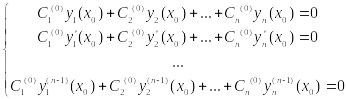, причём не все С_i⁽⁰⁾ одновременно равны 0, i = {1, …, n}. Т.к. у₁(х), у₂(х), ..., у_n(x) решения ЛОДУ, то линейная комбинация С₁⁽⁰⁾ у₁(х) + С₂⁽⁰⁾ у₂(х) + ... + С_n⁽⁰⁾ у_n(x) = y(x) также явл. решением ЛОДУ. В силу равенств в точке х₀ наше решение обращается в 0. Т.к. коэф. линейного оператора непрер., то в силу единственности решения по теор. Пикара у(х) 0, т.е. мы имеем равенство С₁⁽⁰⁾ у₁(х) + С₂⁽⁰⁾ у₂(х) + ... + С_n⁽⁰⁾ у_n(x) = 0, где не все С_i⁽⁰⁾ одновременно равны 0, i = {1, …, n}. А это значит, что у₁(х), у₂(х), ..., у_n(x) л.з. ?!

<=) Если W(x) ≠ 0 (х)ϵ[a,b], то л.н. решений у₁(х), у₂(х), ..., у_n(x) => из предыд. теорем.◄

Зам. Однако оказывается, что для установления л.н. n решений ур-ия (5) достаточно убедиться в том, что W(x) необращается в 0 хотя бы в одной точке [a,b]. Это вытекает из след. св-в определителя Вронского n решений ЛОДУ n-ого порядка: 1. Если определитель Вронского n решений ур-ия равен 0 в одной точке х = х₀, где х₀ ϵ[a,b], при условии, что все коэф. линейного оператора непрер., то он равен 0 и во всех точках точках этого промежутка. 2. Если определитель Вронского n решений ур-ия не равен 0 в точке х = х₀, где х₀ ϵ[a,b], то он отличен от 0 и во всех точках этого отрезка.

Теор. Для л.н. n решений ур-ия на [a,b], где все коэф. линейного оператора непрер. Н. и Д., чтобы их определитель Вронского был отличен от 0 хотя бы в одной точке этого промежутка.

Опр. Совокупность n решений ЛОДУ, определ. и л.н. на [a,b] наз. фундаментальной системой решений (ФСР) на [a,b].

Из предыд. теорем => для того чтобы с-ма n решений была фундаментальной Н. и Д., чтобы определитель Вронского этих решений был отличен от 0 хотя бы в одной точке промежутка непрерывных коэф. ур-ия.

Теор. Если коэф. ур-ия непрер. на I = [a,b], то существует ФСР, определённых на I.

►Пусть х₀ϵ[a,b], решение ур-ия существует по теор. Пикара. Построим это решение. Пусть у₁(х) – решение, удовл. след. нач. усл.: у₁(х₀) = 1, у₁'(х₀) = 0, ..., у₁^(n-1)(x₀) = 0; у₂(х) – решение, удовл. след. нач. усл.: у₂(х₀) = 1, у₂'(х₀) = 0, ..., у₂^(n-1)(x₀) = 0; ...; у_n(х) – решение, удовл. след. нач. усл.: у_n(х₀) = 1, у_n'(х₀) = 0, ..., у_n^(n-1)(x₀) = 0. Тогда определитель Вронского этих решений: , тогда у₁(х), у₂(х), ..., у_n(x) - л.н. и явл. ФСР◄