37.Нормальные с-мы ду. Общие понятия. Механическая интерпретация. Геометрическая интерпретация.

Совокупность соотношений вида: 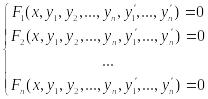(1), где у₁,у₂,...,у_n – искомые ф-ции от независим. перемен. х наз. с-мой обыкнов. ДУ 1-го порядка.

Будем предполагать ф-ции F₁,F₂,…,F_n такими, что с-ма (1) разрешима относит. производной от искомой ф-ции.

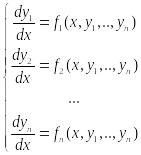(2) – нормальная с-ма ДУ. Число ур-ий вход. в с-му (2) наз. порядком с-мы (2).

Если правые части (2) л.з. от искомых ф-ций у₁,у₂,...,у_n, т.е. с-ма (2) имеет вид: 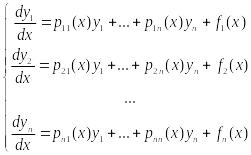(3) – линейная с-ма ДУ, где р_kl(x) – заданные ф-ции, k={1,…,n},l={1,…,n}.

Если правые части (2) не зависят явно от х, т.е. (2) имеет вид: 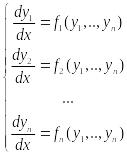(4) – автономная, или стационарная с-ма ДУ.

у₁ = ϕ₁(х), у₂ = ϕ₂(х), ..., у_n = ϕ_n(х) (5) определ. и непрер. дифференц. в интервале [a,b] наз. решением с-мы (1) на [a,b], если оно обращает все ур-ия с-мы (1) в тождетсва.

Геометрическая интерпретация норм. с-мы. Будем рассматривать как координаты точки в n+1 пространстве, тогда решение ур-я (5) соотв-т некоторая кривая. Она наз-ся интегральной кривой. Пусть правые части сис-мы (2) определены и конечны в некоторой обл G- измерения переменных . Проведём к каждой точке обл. G отрезок, направляющие косинусы кот. пропорциональны (1) и значениями правых частей с (2) в этой точке. Получим поле направлений. Всякая интегральная кривая си-мы (2) обладает тем св-ом, что в каждой её точке направление касательных совпадает с направлением поля, определяемыми системой (2) в этой точке.

Механическая интерпретация норм. с-мы.

Примем в норм. с-ме за независим. переменную – время t, а за искомую ф-цию х₁, х₂, ..., х_n. Правую часть обозначим через Х. Тогда получим норм. с-му вида: 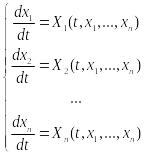(6). Решениям с-мы х₁ = х₁(t), х₂ = х₂(t), …, х_n = х_n(t) соответствует движение точки в n-мерном пр-ве (х₁, х₂, ..., х_n) – фазовое пр-во. Кривая, описываемая в этом пр-ве, движущ. точкой наз. траекторией. Взаимосвязь между траекторией и движением состоит в том, что траектория есть проекция движения, располож. в (n+1)-мерном пр-ве.

Ур-ия х₁ = х₁(t), х₂ = х₂(t), …, х_n = х_n(t) (7) – параметрические ур-ия траектории движения. Эти ур-ия не только определяют ГМТ, но и определяют положение точки в данный момент времени. Они показывают как происходит движение точки на траектории с течением времени. Если все ф-ции х_i(t), i = {1, …, n} представляют собой постоянные величины, то в этом случаи движение (7) выраж. в состоянии покоя, а траектория движения – это точка.

Общее решение.

Семейство решений с-мы (2) зависят от n произвольных постоянных С₁, С₂, ..., С_n : 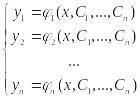(11) обычно наз. общим решением этой с-мы. Геометрически семейство представляет собой семейство интегральных кривых (n+1)-мерном пр-ве, зависящ. от n параметров.

Пусть обл. D в пр-ве (х, у₁,у₂,...,у_n) в каждой точке кот. имеет место существование и единств. задачи Коши с-мы (2).

Опр. Совокупность n ф-ций, определ. в некот. обл. изменения переменных (х, С₁, ..., С_n), имеющих непрер. частные производные по х наз. общим решением с-мы (2) в обл. D, если с-ма (11) разрешима относительно произвольных постоянных С₁, ..., С_n в области D так что при любых значениях (х, у₁, ...,у_n) ϵD с-мы (11) определяются знач. С₁, С₂, ..., С_n:

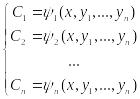(12) и если совокупность n ф-ций (11) явл. решением с-мы (2) при всех знач. произв. постоянных С₁, С₂, ..., С_n, определяемых формулой (12) (х, у₁, ..., у_n)ϵD.

Частное решение.

Опр. Если решение с-мы (2) состоит только из точек единств. решения задачи Коши для этой с-мы, то такое решение наз. частным решением. Решения, получ. из (11) при частных числовых значениях произвольных постоянных С₁, С₂, ..., С_n, включ. будет очевидно частным решением.

Особое решение.

Опр. Решение с-мы (2), в каждой точке кот. нарушается единств. задачи Коши наз. особым решением.

38.С-мы ДУ. Основные понятия. Теорема существования и единственности задачи Коши.

Совокупность соотношений вида: (1), где у₁,у₂,...,у_n – искомые ф-ции от независим. перемен. х наз. с-мой обыкнов. ДУ 1-го порядка.

Будем предполагать ф-ции F₁,F₂,…,F_n такими, что с-ма (1) разрешима относит. производной от искомой ф-ции.

(2) – нормальная с-ма ДУ. Число ур-ий вход. в с-му (2) наз. порядком с-мы (2).

Если правые части (2) л.з. от искомых ф-ций у₁,у₂,...,у_n, т.е. с-ма (2) имеет вид: (3) – линейная с-ма ДУ, где р_kl(x) – заданные ф-ции, k={1,…,n},l={1,…,n}.

Если правые части (2) не зависят явно от х, т.е. (2) имеет вид: (4) – автономная, или стационарная с-ма ДУ.

у₁ = ϕ₁(х), у₂ = ϕ₂(х), ..., у_n = ϕ_n(х) (5) определ. и непрер. дифференц. в интервале [a,b] наз. решением с-мы (1) на [a,b], если оно обращает все ур-ия с-мы (1) в тождетсва.

Задача Коши.

Для с-мы (2) задача Коши ставится след. образом: среди всех решений сис-мы (2) найти такое решение у₁ = у₁(х), у₂ = у₂(х), …, у_n = у_n(х) (8), в кот. ф-ции у₁(х), у₂(х), ..., у_n(х) принимают заданные числовые значения у₁⁽⁰⁾, у₂⁽⁰⁾,..., у_n⁽⁰⁾ при заданном числовом значении х₀, т.е. у₁(х₀) = у₁⁽⁰⁾, у₂(х₀) = у₂⁽⁰⁾, ..., у_n(х₀) = у_n⁽⁰⁾ (9). Числа у₁⁽⁰⁾, у₂⁽⁰⁾,..., у_n⁽⁰⁾ наз. начальными знач. независим. перемен.

Достаточное условие существования и единственности решения задачи Коши.

Теор. Пусть задана нормальная с-ма (2) и поставлены условия у₁= у₁⁽⁰⁾, у₂= у₂⁽⁰⁾, ..., у_n= у_n⁽⁰⁾ при х = х₀ (10). Пусть ф-ции, стоящие в правых частях с-мы (2) определены в некот. замкнутой, огранич. обл. R: |x-x₀| ≤ a, |у₁- у₁⁽⁰⁾| ≤ b, |у₂- у₂⁽⁰⁾| ≤ b, …, |у_n- у_n⁽⁰⁾| ≤ b c точкой (x₀, у₁⁽⁰⁾, ..., у_n⁽⁰⁾) внутри, где a, b – заданные числа. Ф-ция удовл. тогда условиям:

1) правые части f_i(x, y₁, …,y_n) i = {1, …, n} непрер. по всем своим аргументам, а следовательно огранич. |f_i(x, y₁, …,y_n)| ≤ M, i = {1, …, n}, M – некоторая const, M > 0.

2) ф-ции f_i(x, y₁, …,y_n) имеют огранич. частные производные по аргументам y₁, …,y_n, т.е. 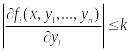, i = {1, …, n}, l = {1, …, n}, k – некоторая положит. const.

Тогда с-ма (2) имеет единств. решение (8), удовл. нач. условиям (10) в интервале |x-x₀| ≤ h, где h = min{a, }.