33.Теорема Пикара (док-во сходимости последовательности приближённых решений).

Дано:

= f(x,y) (1) y(x₀) = y₀ (2)

1) D = {(x,y) : |x-x₀| ≤ a, |y-y₀| ≤ b}}, где a, b – некоторые известные положит. числа, из св-в непрер. ф-ции замкнут. обл. => такого числа М, что для всех точек (x,y)ϵ D : |f(x,y)| ≤ M.

2) |f(x,y₁) - f(x,y₂)| ≤ L |y₁ – y₂|, где L – постоянная Липшица.[ Условие Липшица: если для любых точек х и х', принадлежащих отрезку [а, b], приращение функции удовлетворяет неравенств ∣f(x) — f(x')∣ ≤ L∣х - х'∣^α, где 0 < α ≤ 1 и L — некоторая постоянная].

Ǝ У(х) удовл. нач. условиям у(х₀) = у₀ ,определённое и непрер. диф-мое для знач. х из интервала |x-x₀| ≤ h, где h = min{a, } и х не выходит из обл. D.

Док-во.

3) у_k(x₀) = x₀. Покажим, что Ǝ предел посл-стей (у_n(x)), обозначим его У(х) = и покажим, что посл-сть приближений (4):

...

сходится равномерно на |x-x₀| ≤ h.

Рассмотрим функциональный ряд, k-ая частичная сумма которого равна у_k(x): y₀ + (y₁(x)-y₀) + (y₂(x)-y₁(x)) + … + (y_n(x)-y_n-1(x)) + … (5), S_n = y_n(x). Доказав сходимость (5) док-ем Ǝ предела пос-сти приближений y_n(x) и если сх. будет равномерной, то пос-сть будет сх. к непрер. ф-ции.

Оценим абсолютные величины членов ряда (5): (*)

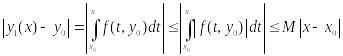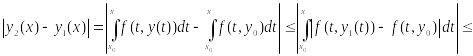
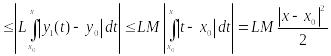
Аналогично: 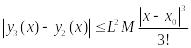. Докажем, что для любого n>0 справедливо: 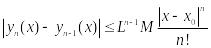(**). Для этого применим ММИ, при условии справедливости нер-ва (**) справедливо нер-во для (n+1):

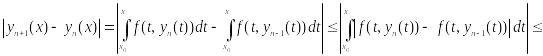
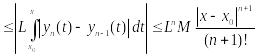(6).

Следовательно (**) справедливо для любых n, если |x-x₀| ≤ h. Обозначим (**) для разл. n через (7).

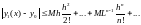_(8).

_{Таким образом, члены функционального ряда (5) меньше ряда с положительными членами.}

_{Этот ряд сходится по признаку Д'Аламбера}

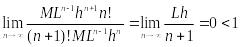
_{Так как все члены ряда (5) по абсолютно величине меньшей членов сходящейся числового ряда, то (5) по пр. Вейерштрасса сходится равномерно для всех х,удовлетворю неравенству .}

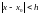_{Каждый член ряда (5)-неперывная ф-ция от х. Так как интеграл есть ф-ция непрерывная( ф-ция переменного предела), то существует ,где У(х) удовлетворяет начальному условию, график этой функции не выходит из области Д}

_{Действительно,}

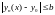
_{Переходя к пределу в последнем неравенстве, получим: ,а это и значит, что график функции не выходит из области D.}

34.Теорема Пикара (док-во существования решения задачи Коши).

Дано:

= f(x,y) (1) y(x₀) = y₀ (2)

1) D = {(x,y) : |x-x₀| ≤ a, |y-y₀| ≤ b}}, где a, b – некоторые известные положит. числа, из св-в непрер. ф-ции замкнут. обл. => такого числа М, что для всех точек (x,y)ϵ D : |f(x,y)| ≤ M.

2) |f(x,y₁) - f(x,y₂)| ≤ L |y₁ – y₂|, где L – постоянная Липшица.[ Условие Липшица: если для любых точек х и х', принадлежащих отрезку [а, b], приращение функции удовлетворяет неравенств ∣f(x) — f(x')∣ ≤ L∣х - х'∣^α, где 0 < α ≤ 1 и L — некоторая постоянная].

Ǝ У(х) удовл. нач. условиям у(х₀) = у₀ ,определённое и непрер. диф-мое для знач. х из интервала |x-x₀| ≤ h, где h = min{a, } и х не выходит из обл. D.

Док-во.

_{Покажем, что 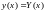есть решение интегрального уравнения (3). Для этого покажем сначало, что предел 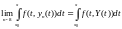, то есть допустим предельный переход под знаком интеграла.}

_{Так как yn(x) сх. равномерно к Y(x) на промежутке , то по-любому Е>0, будет выполнятся неравенство: .Для любого х из одновременно.}

_{Оценим разность:}

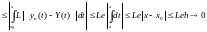
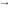
_{Отсюда следует, что .Из предыдущего следует, что . И в равенстве, определ. 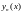, перейдём к пределу при н-к бескон.}

_{, данная ф-ция явл решением интегрального уравнения (3).Значит решение ур-я (1),определённом и непрерывно дифф. при и удовлетвор. Начальному усл (данная ф-ция допускает производную по х,так как в правой части уравнения стоит интеграл от непрерывной функции,допускающая производную по верхнему пределу).}