23. Линейные неоднородные ду n-го порядка с постоянными коэффициентами и специальной правой частью. Специальная правая часть как произведение экспоненты и выражения с синусом и косинусом.

(1),где -постоянные действительные числа, i=0,n-1

f(x)-непрерывная на некотором промужутке.

Построим ФСР соответствующего ДУ можно решение ур-я (1),следуя методу Лагранжа,найти в квадратурах.

Для некоторых частных видов f(x) удаётся найти частное рещение (1)без квадратур.

В силу т.О структуре решения ЛНДУ нам нужно найти к-либо частное решение этого уравнения и сложив егос общим решением ОДУ,получим общее решение (1).

Пусть правая часть уравнения имеет вид: * ,хотя бы 1 из них имеет степень =m .Заменяя , по формуле Эйлера: =

Равенство * можно переписать: ==,причём собирая коэ-ты при aльфа и бета==

представляет собой сумму двух слога емых рассмотренного вида,т.е имеет место 2 случая:

1 случай: альфа и бета таковы,что число не явл корнем ХУ,тогда частное решение будем искать в виде : (**)

, - полиномы к-ой степени с неопределенными коэ-ми

Если явл. S- кратным корнем ХУ, то частое решение найдётся в виде (***): , где с-кратность корня.

Приведя (**) и (***) к вещественному виду, получим след правило нахождения частного решения уравнения (1), когда правая часть имеет вид (*)

1. В 1 случае, если не явл. Корнем ХУ, то часное решение найдётся в виде:

2. если явл. S-кратным корнем ХУ, если , то часное решение найдётся в виде: ,где P,Q - палиномы с неопределёнными коэф.

В обоих случаях определяются подстановкой в (1).

24.Приложение ДУ в физике. Свободные колебания в среде без сопротивления.

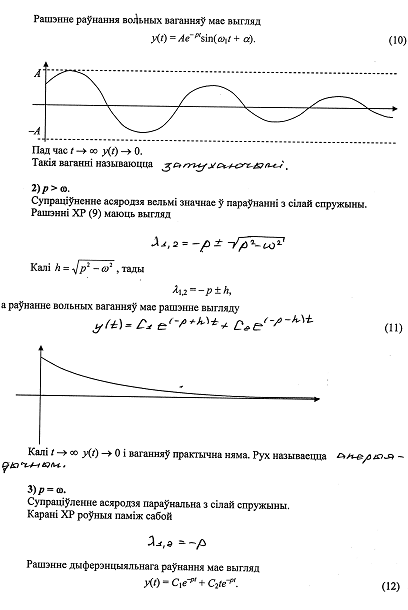
25.Приложение ДУ в физике. Свободные колебания в среде с сопротивлением.

26.Приложение ДУ в физике. Вынужденные колебания в среде без сопротивления.

27.Приложение ДУ в физике. Вынужденные колебания в среде с сопротивления.

28.Введение элементарных ф-ций с помощью ДУ. Показательная ф-ция (экспонента).

29.Введение элементарных ф-ций с помощью ДУ. Тригонометрические ф-ции.

НЕТ В БИЛЕТАХ!!!!УРААААА!!!

30.Условия Липшица. Теорема Пикара (формулировка).

Условие Липшица

Рассмотрим функцию , определенную и непрерывную в прямоугольнике К: _.

О пр. Если для любого и любых двух значений и переменной :

, существует такое, не зависящее от х число , что выполнено неравенство: (*), то говорят, что функция в области К удовлетворяет условию Липшица с постоянной L.

Зам. 1. Если в области К имеет непрерывную частную производную , то всегда найдется такое L, что условие (*) будет выполнено. Действительно, тогда по формуле Лагранжа (**), – лежит между и .

В силу непрерывности в К и замкнутости области К, в К ограничена, т.е. , где L – некоторая константа. В этом случае, в частности, за L можно принять .

2. Условие Липшица (*) более слабое, чем существование частной производной , так как оно может быть выполнено и в том случае, когда существует не всюду в К.

Теор. Пикара Пусть дано уравнение = f(x,y) (1) и начальные условия у = у₀, х = х₀. Если ф-ция f(x,y) удовл. 2-м усл.: 1) непрер. по обеим перемен. в замкнут. обл. D = {(x,y) : |x-x₀| ≤ a, |y-y₀| ≤ b}, где a, b – некоторые известные положит. числа, из св-в непрер. ф-ции замкнут. обл. => такого числа М, что для всех точек (x,y)ϵ D : |f(x,y)| ≤ M. 2) f(x,y) в обл. D удовл. условию Липшица по перемен. у : |f(x,y₁) - f(x,y₂)| ≤ L |y₁ – y₂|, где L – постоянная Липшица. Тогда ! решение у(х) удовл. начальному условию у(х₀) = у₀ (2), определённое и непрер. диф-мое для знач. х из интервала |x-x₀| ≤ h, где h = min{a, } и х не выходит из обл. D.