1.Обыкновенные ду: определение, порядок, решение, интегральная кривая, интегрирование, интегрирование в квадратурах.

Пусть ф-ция F – ф-ция (n+2) переменных. Надо найти ф-цию у(х), удовл. на некот. промежутке I ур-ию F(x, y(x), y'(x), …, y⁽ⁿ⁾(x)) = 0. (1)

Опр. Обыкновенным ДУ наз. соотношение вида F(x, y(x), y'(x), …, y⁽ⁿ⁾(x)) = 0, где F – известная ф-ция, х – независимая перемен., у(х) – неизв. ф-ция.

Опр. Порядком ДУ наз. порядок старшей производной неизв. ф-ции у = у(х), вход. в уравнение.

Опр. Ф-ция у(х) наз. решением ДУ, если она n раз непрер. диф-ма на некотором промежутке I и если хϵI, то ф-ция у(х) удовл. ур-нию (1).

Опр. График решения ДУ наз. интегральной кривой этого ур-ия.

Опр. Процесс нахождения решения ДУ наз. интегрированием ДУ.

Пр. Найти кривые, у которых тангенс угла между касательной и положит. направлением оси Ох равен абсциссе в точке касания.

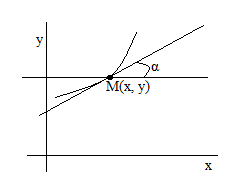
= x

dy = xdx

dy = d => y = + C, C ϵ R.

Зам. Когда задачу нахождения всех решений ДУ удаётся свести к вычислению конечного числа интеграллов, производных от известных ф-ций, а также алгебраических операций над ними, то говорят, что уравнение интегрируется в квадратурах.

2.Задачи, приводящие к ду.

Задача. В благоприятных для размножения условиях находится некоторое количество N₀ бактерий. Из эксперимента известно, что скорость пропорц. их количеству. Найти зависимость роста числа бактерий в течение времени.

Решение. N(t) – кол-во размнож-ся бактерий с течением времени t. N(0)=N₀. Будем считать, что N(t) измеряется во времени, непрер. диф-ма. Тогда скорость размножения это = kN(t) (1). Коэф. k зависит от выбора бактерий и условий, в кот. они находятся.

Найти решение N = N(t) ур-ня (1) для кот. N(0)=N₀.

N(t) > 0 = kdt => d lnN(t) = kdt => lnN(t) = kt + C₁ , где C₁ - const, C₁ = ln C, C > 0 =>

N(t) = Ce^kt . t=0 N(0)=N₀ => C = N(0)=N₀. N(t) = N₀e^kt.

Т.е. численность бактерий возрастает по экспоненциальному закону.

Ур-ие (1) описывает различные процессы и зависимости между величинами. Решением (1) явл. ф-ции вида N(t) = Ce^kt, где С – произв. число.

Док-ем, что ур-ие вида = ky (2) имеет решение только такого вида y = Ce^kx и др. нет.

Рассмотрим ф-цию y=ϕ(x) и пусть оно некоторое решение (2). Далее рассмотрим ф-цию Ф(х) = ϕ(x)∙e^-kx и найдём её производную: = ∙ e^-kx + ϕ(х)∙(-k)e^-kx = e^-kx ( - k∙ϕ(х)). Т.к. ϕ(х) явл. решением (2), то выражение в скобках равно 0, т.е. = 0 => Ф(х) = С – const.

Получаем С = ϕ(х)∙e^-kx => ϕ(х) = C∙e^kx .

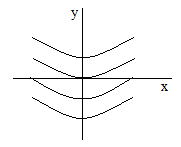
Мн-во решений обладает св-вом: графики ф-ций у = C∙e^kx со всевозможными числовыми знач. С покрывают всю плоскость, причём через каждую точку пл-сти проходит график единств. такой ф-ции.

Выделим из этих решений решение проходящее через точку (х₀,у₀). Для определения С получим уравнение: у₀ = С∙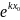 , которое имеет единственное решение С = у₀ , частное решение: у = у₀∙ .

3.ДУ 1-го порядка: формы записи решения и ннтегралы, геометрическая интерпретация частного и общего решений.

Общий вид ДУ 1-ого порядка F(x, y, y') (1). Частное уравнение = f(x,y) (2), где действит. ф-ция f(x,y) задана в некоторой обл. D. (2) наз. уравнением разрешённым относительно производной. На виду с (2) всегда будем рассматр. = (2'). Использ. последнее в окрестности тех точек, где ф-ция f(x,y) обращается в .

Вместо (2) и (2') целесообр. рассматр. ур-ие dy – f(x,y)dx = 0 (3). Обе перемен. х и у входят в это ур-ие равноправно и любую из них можно рассматр. как независимую перемен. Умножив обе части ур-ия (3) на некот. ф-цию N(x,y) получим ур-ие: М(х,у)dx + N(x,y)dy = 0 (4), где M(x,y) = -f(x,y)∙N(x,y). = - и = - . Симметричная форма: = .

Рассм. ур-ие = f(x) (5). В этом случаи, если f(x) определена и непрер. на промежутке I, то каждая первообразная ф-ции f(x) на I явл. решением (5). Из матем. анализа известно, что х ϵ I все первообразные содерж. в формуле у(х) = (6). Если в (6) заместо запишем , то решение (5) м.б. записано в виде у(х) = (7). Решение ур-ия (5) имеет вид у = ϕ(х, С) (8) - общее решение.

Опр.Ф-ция у = ϕ(х,С), определённая в некоторой обл. изменения перемен. х и С, и имеющая непрер.частную производную по х наз. общим решением (2) в обл. D(обл. в которой (2) имеет единств. решение), если:

1)соотношение у = ϕ(х,С) (2) разрешимо относительно С при всех знач. у из обл. D, т.е. С = ψ(х,у) (3)

2)для всех знач. х и у из D (3) даёт такое знач. С, включая , при кот. ф-ция ϕ(х,С) будет явл. решением (1).

Суть опр. состоит в след.: пусть дано семейство кривых F располож. в D и зависящих от одного параметра С. Если про каждую кривую из F известно, что она явл. интегральной кривой ур-ия (1) и все кривые из F в их совокупности покрывают D, то F – общее решение (1) в обл. D.

В дальнейшем покажим, что (2) при достаточно общих условиях , их бесконечное мн-во, а именно семейство у = ϕ(х).

Решение, кот. получается из общего решения при конкретном С наз. частным решением.

Решение, кот. нельзя получить из общего решения при конкретном С наз. особым решением.

Соотношение вида Ф(х,у,С) = 0, кот. неявно определяет общее решение наз. общим интеграллом ДУ.

Если требуется найти решение, кот. удовл. дополнительным условиям, то такая формулировка задачи носит название задача Коши: [само ДУ + дополн. усл.].

Пусть х и у декарт. прямоуг. координаты на пл-сти. Каждой точке (х,у)ϵD, где определена и конечна ф-ция f(x,y), ур-ие ставит в соответствие определ. знач. , явл. тангенсом угла наклона, образов. касат. к интегр. кривой с осью Ох.

Т.обр., каждой точке (х,у)ϵD, ДУ ставит в соответствие определённое ур-ие, т.е. в обл. определения ф-ции f(x,y) ДУ задаёт поле направлений. С геометрической точки зрения задача интегрир. ДУ м.б. сформулир. так: найти такие кривые, касательные к кот. совпадают с направлением поля в этой точке.

Опр. Кривая, в каждой точке кот. наклон поля, определ. ДУ, один и тот же наз. изоклиной.

Уравнение изоклин имеет вид: f(x,y) = k, где k – постоянное число.