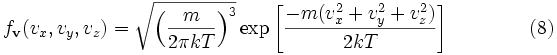Вопрос 19.
где
k является отношением газовой постоянной
R к числу Авогадро, а i - число степеней
свободы молекул. Основное уравнение
МКТ связывает макроскопические параметры
(давление, объём, температура) газовой
системы с микроскопическими (масса
молекул, средняя скорость их движения).
Вывод основного уравнения МКТ
Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём.
Обозначим
скорость движения vx, тогда перед
столкновением со стенкой сосуда импульс
частицы равен mvx, а после - − mvx, поэтому
стенке передается импульс p = 2mvx. Время,
через которое частица сталкивается с
одной и той же стенкой, равно
.
Отсюда следует
,
поэтому давление
,
соответственно
и
Таким образом, для большого числа частиц
верно следующее:
аналогично
для осей y и z.
Поскольку
,
то
.
Отсюда
или
Пусть
— средняя кинетическая энергия молекул,
а Ek — полная кинетическая энергия всех
молекул, тогда:
,
откуда
Температура - физическая величина, характеризующая состояние теплового равновесия системы тел: все тела системы, находящиеся друг с другом в тепловом равновесии, имеют одну и ту же температуру.
Давле́ние (P) — физическая величина, характеризующая состояние сплошной среды и численно равная силе , действующей на единицу площади поверхности перпендикулярно этой поверхности.
Вопрос 20
Под
внутренней энергией термодинамической
системы понимают кинетическую энергию
теплового движения ее молекул и
потенциальную энергию их взаимодействия.
Она зависит от параметров состояния
V,T . Внутренняя энергия идеального
одноатомного газа прямо пропорциональна
его абсолютной температуре:
Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные).
В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:
Если
система молекул находится в тепловом
равновесии при температуре T, то средняя
кинетическая энергия равномерно
распределена между всеми степенями
свободы и для каждой степени свободы
молекулы она равна
Вопрос 21.
Молекулы газа вследствие теплового движения испытывают многочисленные соударения друг с другом. При каждом соударении скорости молекул изменяются как по величине, так и по направлению. В результате в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям, зависящее от абсолютной температуры T. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а величины скоростей подчиняются определенной закономерности. Распределение молекул газа по величине скоростей называется распределением Максвелла. Характерным параметром распределения Максвелла является так называемая среднеквадратичная скорость vкв = <v2>1/2, где <v2> означает среднее значение квадрата скорости.
