Вопрос 12.

Колебательное движение - периодическое или почти периодическое движение тела, координата, скорость и ускорение которого через равные промежутки времени принимают примерно одинаковые значения. Механические колебания возникают тогда, когда при выводе тела из положения равновесия появляется сила, стремящаяся вернуть тело обратно. Свободные колебания являются незатухающими, если не происходит рассеяния энергии в окружающее пространство. Однако реальные колебательные процессы являются затухающими, так как на колеблющееся тело действуют силы сопротивления движению. Гармоническими называются колебания, происходящие по закону синуса или косинуса: где x(t) - смещение системы в момент t, A - амплитуда, ω - циклическая частота колебаний.

Вопрос 13.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.

уравнения свободных колебаний пружинного маятника. 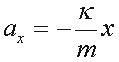, то есть пропорционально координате с отрицательным коэффициентом пропорциональности. Рассмотрим движение небольшого бруска массой m, расположенного на гладкой горизонтальной поверхности и прикрепленного к неподвижному упору с помощью легкой пружины жесткости k. На основании этого мы делаем обоснованный вывод: в рассматриваемой системе брусок совершает гармонические колебания Частота этих колебаний не зависит от их амплитуды и легко находится из сравнения уравнений (2) и (3), идентичность которых требует выполнения условия

Вопрос 14.

Амплиту́да — максимальное значение смещения или изменения переменной величины при колебательном или волновом движении. Неотрицательная скалярная величина, измеряется в единицах, зависящих от типа волны или колебания.

Частота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — , или . Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz). Величина, обратная частоте, называется периодом.

Циклическая частота связана с частотой колебаний соотношением . В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (рад/с, rad/s) .

Фа́за колеба́ний — аргумент периодической функции описывающей гармонический колебательный процесс (ω— угловая частота, t— время, — начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0). Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода).

Периодом Т называется время одного полного колебания. По истечении времени Т повторяются значения всех физических величин, характеризующих колебания.

Вопрос 15.

Энергия гармонического колебательного движения. При совершении колебания кинетическая и потенциальная энергия и будет переменны. Потенциальная энергия измеряется работой силы, вызывающей смещение х, и эта сила равна возвращающей силе F и обратно ей по направлению. Тогда , где , следовательно . Но , а поэтому потенциальная энергия тела, совершающего гармоническое колебательное движение, будет равна . Так как скорость колеблющегося тела то его кинетическая энергия будет Полная энергия тела, совершающего гармоническое колебательное движение, Равна

Следовательно, полная энергия колеблющегося тела пропорциональна квадрату амплитуды и не меняется в течение колебательного процесса.