Вопрос 1.
ТРАЕКТОРИЯ, ПУТЬ И ПЕРЕМЕЩЕНИЕ
Траектория - линия, которую описывает при своем движении материальная точка.
Путь – (I) это длина траектория движения тела.
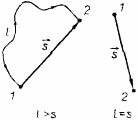
Перемещением
тела
называют вектор, соединяющий начальное
положение тела с его конечным положением.
ЗАКОН ДВИЖЕНИЯ
МТ материальной
точки - зависимость от времени её
радиус-вектора
Скорость материальной точки есть её перемещение за бесконечно малый промежуток времени, отнесенное к единице времени
.
Скорость - векторная
величина, характеризующая направление
и быстроту перемещения материальной
точки:
Вопрос 2
Равноускоренным называется движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково.
Ускорением тела называют отношение изменения скорости тела ко времени, за которое это изменение произошло.
Ускорение характеризует быстроту изменения скорости.
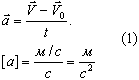
Ускорение - векторная величина. Оно показывает, как изменяется мгновенная скорость тела за единицу времени.
Зная
начальную скорость тела и его ускорение,
из формулы (1) можно найти скорость в
любой момент времени:
Вопрос 3.
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки.
Угловая
скорость (w) – величина, равная отношению
угла поворота радиуса, на котором
находится вращающаяся точка, к промежутку
времени, за который произошел этот
поворот:
Связь между линейной и угловой скоростями: v= wr.
Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе.
Линейная
скорость
Вопрос 4.
Ускорение при криволинейном движении: нормальное, тангенциальное, полное.
Тангенциальная
составляющая ускорения - характеризует
быстроту изменения скорости по модулю
Нормальная
составляющая ускорения - направлена по
нормали к центру кривизны - характеризует
быстроту изменения скорости по направлению
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих .
При движении по окружности с постоянной по величине линейной скоростью v тело испытывает направленное к центру окружности постоянное центростремительное ускорение
a = v2/R,
г
О
В
А
По
определению
На
рисунке треугольники, образованные
векторами перемещений и скоростей,
подобны. Учитывая, что |r1| = |r2| = R и |v1| =
|v2| = v, из подобия треугольников находим:
откуда
Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом j, измеряемым в радианах (рад), причем
x = R cos(j + j0), y = R sin(j + j0),
где j0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).
В случае равномерного вращения угол j, измеряемый в радианах, линейно растет со временем:
j = wt,
где w называется циклической (круговой) частотой. Размерность циклической частоты: [w] = c-1 = Гц. Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью. Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:
x = R cos(wt + j0),
y = R sin(wt + j0).
Время, за которое совершается один оборот, называется периодом T.
Частота
n = 1/T.
Размерность частоты: [n] = с-1 = Гц.
Связь циклической частоты с периодом и частотой: 2p = wT, откуда
w = 2p/T = 2pn.
Связь линейной скорости и угловой скорости находится из равенства: 2pR = vT, откуда
v = 2pR/T = wR.
Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:
aц = v2/R = w2R = 4p2n2R = 4p2R/T2.