6.2. Дисперсия, её математические свойства и способы расчёта

Дисперсия наряду со средним квадратическим отклонением являются мерилом надёжности средней величины. Чем меньше дисперсия и среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую ею совокупность.

Дисперсия обладает рядом свойств (доказываемых в математической статистике), которые часто позволяют упростить расчёты. Эти свойства следующие:

1. Если из всех значений вариант отнять какое-либо постоянное число то дисперсия от этого не изменится.

2. Если все значения вариант разделить на какое-то постоянное число то дисперсия уменьшится от этого в раз.

3. Средний квадрат отклонений от любой величины отличной от средней арифметической всегда больше дисперсии, причём

или

Используя свойства дисперсии, её можно вычислить упрощёнными способами без привлечения формулы, определяющей дисперсию.

Из последней формулы в случае, когда следует

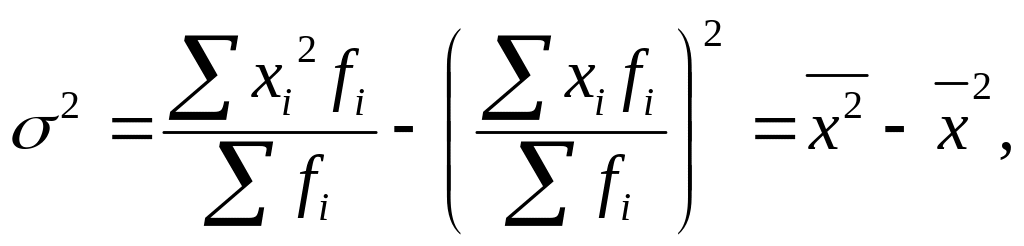
т. е. дисперсия равна разности среднего квадрата признака минус квадрат среднего значения признака. В статистике величины и называют начальными моментами второго и первого порядка, соответственно.

Способ расчёта дисперсии по формуле

называется способом моментов.

В случае расчёта дисперсии интервального вариационного ряда при условии равных интервалов применяется модифицированный способ моментов, или способ отсчёта от условного нуля. Используя второе свойство дисперсии, разделив все варианты на величину интервала , получим

6.3. Виды дисперсий, правило сложения дисперсий и его использование в

анализе факторов

Исчисляя дисперсию изучаемого признака в пределах совокупности и, опираясь в расчётах на общую среднюю, мы не можем определить влияние отдельных факторов, характеризующих колеблемость индивидуальных значений (вариант) признака.

Это можно сделать при помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку-фактору. Причём можно определить три показателя колеблемости признака в совокупности:

- общую (или генеральную) дисперсию;

- межгрупповую дисперсию;

- среднюю внутригрупповых дисперсий.

Общая дисперсия характеризует вариацию признака, которая зависит от всех условий (факторов) в данной совокупности, и исчисляется по формуле

где - общая средняя для всей изучаемой совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых средних около общей средней и вычисляется по формуле

где - численность отдельных групп.

Средняя внутригрупповых дисперсий характеризует случайную, не обусловленную признаком-фактором, вариацию в отдельных группах. Эта вариация возникает под влиянием других не учитываемых факторов и не зависит от признака-фактора, положенного в основу группировки. Она определяется по формуле

,

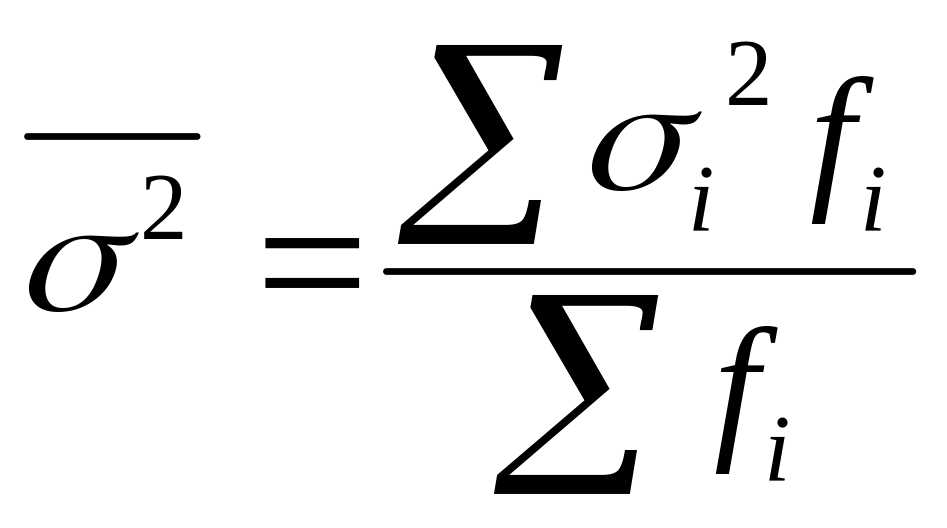где - дисперсия изучаемого признака по каждой отдельной группе.

В математической статистике доказывается правило сложения дисперсий, которое говорит, что общая дисперсия равна сумме межгрупповой дисперсии и средней внутригрупповых дисперсий. Оно записывается в виде формулы

Это правило (закон) сложения дисперсий имеет большую практическую значимость, так как позволяет выявить зависимость вариации от определяющих её факторов при помощи соотношения межгрупповой и общей дисперсии

Это соотношение называется коэффициентом детерминации и определяет процент различий (отклонений) в совокупности, обусловленный признаком-фактором, выбранным для группировки в качестве основного.

Пример. При исследовании производительности труда однородной совокупности рабочих на предприятии была проведена группировка рабочих по размеру заработной платы. В результате статистической обработки данных и расчётов оказалось, что коэффициент детерминации Это означает, что различие в производительности труда отдельных рабочих лишь на 43 % обусловлены фактором заработной платы и, следовательно, на 57 % - остальными факторами (условиями).

В статистике наряду с дисперсией количественного признака определяется дисперсия альтернативного признака. Альтернативными являются признаки (в том числе качественные), которыми обладают одни единицы изучаемой совокупности и не обладают другие. Формула расчёта дисперсии альтернативного признака имеет вид

где доля вариантов, обладающих изучаемым признаком.

Тест 2

В качестве варианта ответа необходимо выбрать вариант, содержащий наиболее полный, правильный и точный ответ на вопрос.

№	Вопрос	Варианты ответа
1	Статистический показатель – это	1) число, адекватно характеризующее явление или процесс 2) количественная характеристика, адекватно отображающая явление в условиях качественной определенности 3) величина, определяемая расчётным путем 4) характеристика явления в условиях качественной определённости
2	Система статистических показателей применяется для	1) комплексного описания статистического объекта 2) получения целостной, всесторонней характеристики изучаемого явления 3) описания определённых сторон изучаемого явления 4) характеристики отдельных единиц совокупности
3	Абсолютный показатель получают путём	1) непосредственного наблюдения первичных данных 2) непосредственного наблюдения и суммирования первичных данных, характеризующих численность совокупности, объём изучаемого явления в конкретных границах места и времени 3) непосредственного суммирования относительных показателей, характеризующих изучаемую совокупность 4) непосредственного применения к числовым данным методов математической статистики
4	Относительные величины динамики характеризуют	1) изменение изучаемых явлений в пространстве, выявляют направление их развития 2) результаты сопоставления одноименных показателей относящихся к разным периодам и объектам наблюдения 3) долю отдельных частей в общем объёме изменяющей во времени совокупности 4) изменение изучаемых явлений во времени, выявляют направление их развития
5	Различают средние	1) групповые и структурные 2) общие и степенные 3) степенные и структурные 4) общие и функциональные
6	Средними величинами называют	1) обобщающие показатели, характеризующие типичный уровень варьирующего признака в расчёте на единицу совокупности 2) обобщающие показатели, характеризующие объём и размер изучаемого явления 3) среднюю гармоническую величину изменяющегося признака 4) средние структурные показатели, характеризующие всю совокупность
7	Формула средней гармонической	1) 2) 3) 4)
8	К структурным средним относят	1) моду и медиану 2) децили и среднюю арифметическую 3) среднюю квадратическую и квартили 4) медиану и среднюю гармоническую
9	Медиана - это	1) величина признака, которая делит вариационный ряд на две равные части 2) наиболее часто встречаемое значение признака 3) величина признака, которая делит численность упорядоченного вариационного ряда пополам 4) половина численности ранжированного вариационного ряда
10	Мода - это	1) наиболее часто встречающееся значение признака у единиц в совокупности 2) наиболее значимая величина признака 3) наиболее выделяемая группа единиц совокупности 4) частота наиболее часто встречающегося значения признака у единиц совокупности
11	Алгебраическая сумма отклонений значений признака от средней арифметической	1) минимальна 2) больше единицы 3) меньше нуля 4) равна нулю
12	Статистический ряд распределения - это	1) упорядоченная совокупность признаков наблюдения 2) упорядоченное расположение единиц совокупности или групп по группировочному признаку 3) совокупность вариант и частот 4) распределение единиц совокупности в определенном порядке
13	Какое значение признака может иметь вариационный ряд распределения совокупности людей по росту	1) рост высокий 2) рост средний 3) рост 182 см 4) рост низкий
14	Варианта - это	1) вариация изучаемого признака в совокупности 2) случай, событие, факт, фиксируемые в наблюдении 3) значение признака, которое принимает единица, не входящая в исследуемую совокупность 4) отдельное значение варьирующего признака, которое он принимает в ряду распределения
15	Связь между частотами и значениями варьирующего признака в распределениях заключаются в том, что	1) с ростом значения признака частота растёт, а потом остаётся постоянной 2) с ростом значения признака частота растёт до определенной величины, а затем уменьшается до нуля 3) с ростом значения признака частота постоянно уменьшается до нуля 4) с ростом значения признака частота уменьшается до определенного значения, а затем остается постоянной
16	Графическое изображение интервального вариационного ряда может производиться с помощью	1) кардиограммы 2) монограммы 3) гистограммы 4) криптограммы
17	Статистический график - это	1) наглядное изображение статистических данных с помощью геометрических линий, фигур, схем, значков и т.д. 2) вид гравюры, изображающей статистические показатели 3) совокупность линий, представляющих собой строки и графы 4) совокупность точек, соединённых прямыми линиями
18	Под вариацией в статистике понимают	1) изменение, колеблемость, различие 2) изменение исследуемого признака в пределах неоднородной совокупности, обусловленное влиянием различных факторов 3) количественные изменения признака в пределах однородной совокупности, которые обусловлены влиянием действия различных факторов 4) показатель, характеризующий меру колеблемости отдельных значений признака внутри изучаемой совокупности
19	К абсолютным показателям вариации относится	1) коэффициент осцилляции 2) коэффициент вариации 3) коэффициент линейного отклонения 4) среднее линейное отклонение
20	К относительным показателям вариации относится	1) коэффициент вариации 2) дисперсия 3) среднее линейное отклонение 4) размах вариации
21	Средняя внутригрупповых дисперсий равна	1) сумме общей и межгрупповой дисперсий 2) разности общей и межгрупповой дисперсий 3) произведению общей и межгрупповой дисперсий 4) отношению межгрупповой и общей дисперсий
22	Коэффициент детерминации определяется через	1) среднее значение признаков и общую дисперсию 2) коэффициент осцилляции и межгрупповую дисперсию 3) межгрупповую дисперсию и общую дисперсию 4) межгрупповую дисперсию и коэффициент вариации

Решение задач

Задача 3. Имеются следующие данные по двум текстильным фабрикам за два месяца:

Фабрика	Май		Июнь
	Выработка одной ткачихи за смену, кв. М	Число ткачих на фабрике	Выработка одной ткачихи за смену, кв. м	Выработка ткани за смену на фабрике, кв. м
1	64	180	62	12000
2	60	220	58	13000

Определить среднюю выработку ткачихи за смену по двум фабрикам в мае и июне. Обосновать выбор средней.

Решение.

1) За май имеются данные по выработке ткачихи за смену (осредняемый признак) и числе ткачих (частота признака) по двум фабрикам (единицам изучаемой совокупности). Поэтому для нахождения средней выработки ткачихи необходимо использовать формулу средней арифметической взвешенной

= 61,8 кв. м ,

где , - выработка ткачихи за смену и численность ткачих на i-ой фабрике.

2) За июнь имеются данные по выработке ткачихи за смену и итоговые показатели выработки ткани за смену на фабрике. Поэтому необходимо использовать формулу средней гармонической взвешенной

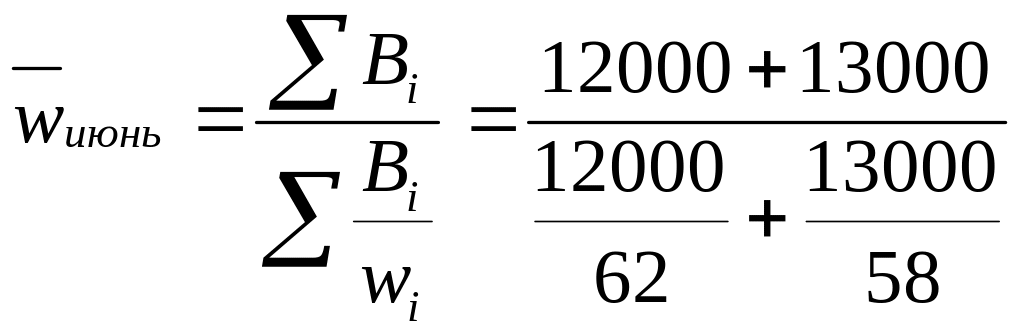= 59,85 кв. м ,

где - выработка ткани на i-ой фабрике за смену.

Задача 4. В результате проведенной группировки получены следующие данные о распределении работников предприятия по заработной плате (в усл. ед.):

Месячная заработная плата	До 200	200 - 240	240 - 280	280-320	320 и выше
Число работников	15	20	25	30	10

Определить: 1) среднее значение заработной платы обычным способом и способом моментов; 2) моду и медиану. Пояснить полученные результаты.

Решение. Имеется интервальный ряд распределения, поэтому необходимо определить серединные значения признака в интервалах. Они равны: 180; 220; 260; 300; 340.

1) Среднее значение заработной платы можно рассчитать по формуле средней арифметической взвешенной

усл. ед.

, - серединные значения интервалов и соответствующие частоты.

2) Для расчёта способом моментов воспользуемся формулой

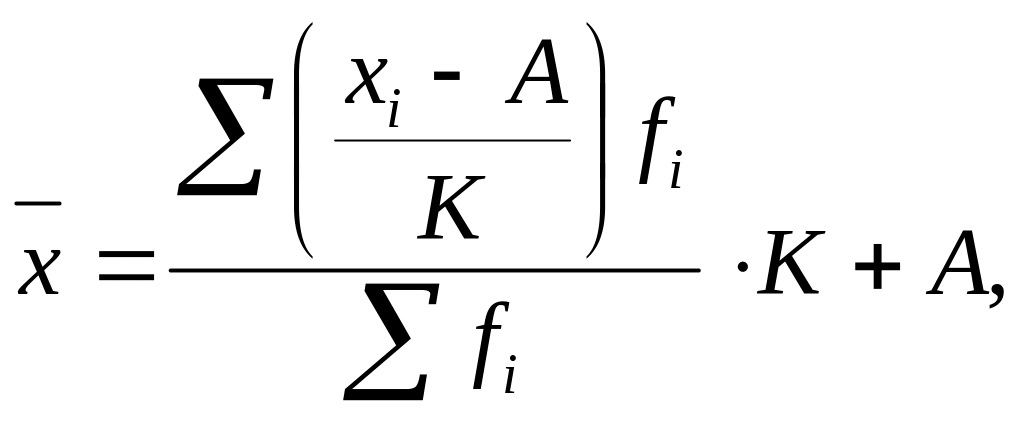
где значения признака будем уменьшать на величину и полученные значения делить на величину

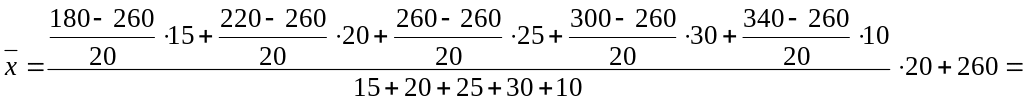
усл. ед.

3) Порядковый номер модального интервала (с наибольшей частотой признака) равен 4.

Мода рассчитывается по формуле

усл. ед.

Мода определяет наиболее часто встречаемое значение признака.

4) порядковый номер медианного интервала

№ .

Медиана рассчитывается по формуле

усл. ед.

Медиана определяет значение признака (месячная заработная плата), которое делит численность упорядоченного ряда на две равные части.

Задача 5. По имеющимся в задаче 4 данным исчислить показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, а также коэффициенты осцилляции, линейного отклонения и вариации.

Решение. Исходными данными для расчёта показателей являются серединные значения интервалов. Размах вариации

усл. ед.

Среднее линейное отклонение

40 усл. ед. =

= .

Дисперсия

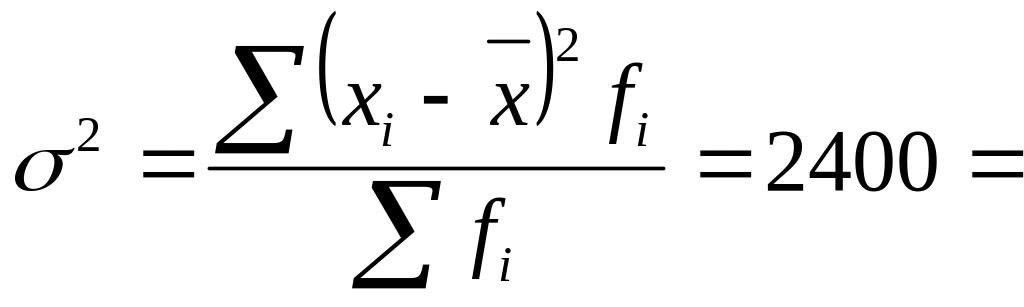
Среднее квадратическое отклонение

усл. ед.

Коэффициент осцилляции

Коэффициент линейного отклонения

Коэффициент вариации

Задача 6. По данным задач 4, 5 определить коэффициент детерминации, если дисперсии в группах работников, распределенных по заработной плате известны и равны, соответственно: 160; 350; 220; 300; 650.

По известным дисперсиям в группах определяется средняя внутригрупповых дисперсий

Используя правило сложения дисперсий, определяем межгрупповую дисперсию

Коэффициент детерминации равен

.

Т.е. на 86% различия в совокупности работников обусловлены группировочным признаком – месячной заработной платой.