
- •Етапи аналізу даних. Класифікація типів змінних. Кількісні, ординальні та номінальні дані та робота з ними.
- •Методи візуалізації даних. Графічні методи експрес-аналізу даних.
- •Генетичний алгоритм. Генетичне програмування.
- •Методи, стадії, задачі Data Mining.
- •Однофакторний дисперсійний аналіз.
- •Ітераційний алгоритм обчислення головних компонент.
- •Дерева рішень. Методи опорних векторів, «найближчого сусіда», Байеса.
- •Правило розбиття
- •Зупинка навчання
- •Правило відсікання
- •Класифікація з учителем у випадку нормальних спостережень.
- •Асоціаційні правила. Послідовне відображення шаблонів даних.
Однофакторний дисперсійний аналіз.
Дисперсійний однофакторний аналіз використовується у дослідженнях зміни результативної ознаки під впливом зміни умов або градацій фактора. Суть математичних перетворень дисперсійного методу полягає в тому, щоб зіставити дисперсії за факторами із дисперсією усіх значень, отриманих в експерименті. Однофакторний аналіз вимагає не менше трьох градацій фактора і не менше двох випробовувань у кожній градації. При проведенні дисперсійного аналізу необхідно перевірити нормальність розподілу досліджуваної випадкової величини і відсутність відмінності дисперсій сукупностей. Це можна виконати методами перевірки статистичних гіпотез. Розглядається дія одиничного фактору А (кількісного чи якісного), котрий приймає k різних значень (рівнів фактора). Найпростіші розрахунки виходять при рівній кількості дослідів на кожному рівні фактора А.
Вихідні дані для однофакторного дисперсійного аналізу з рівним числом паралельних дослідів |
||||
Номер досліду |
Рівні
фактору |
|||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
... |
... |
... |
... |
... |
n |
|
|
... |
|
Дисперсійний аналіз можна провести за наступним алгоритмом:
Обчислити:
суми за стовпцями:
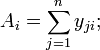
суму квадратів усіх дослідів:
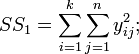
суму квадратів сум за стовпцями, поділену на число дослідів в стовпці:
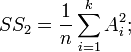
квадрат загальної суми, поділений на число всіх дослідів (коректуючий член):
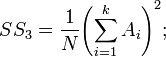
суму квадратів для стовпчика:
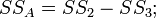
загальну суму квадратів, рівну різниці між сумою квадратів всіх дослідів та коректуючим членом:
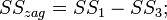
залишкову суму квадратів для оцінки помилки експерименту:
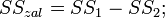
дисперсію
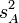 :
:  ;
;дисперсію:
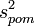 :
: 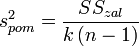 ;
;
Результати розрахунків представити у вигляді таблиці дисперсного аналізу:
Вихідні дані для однофакторного дисперсійного аналізу з рівним числом паралельних дослідів |
||||
Джерело дисперсії |
Число ступенів вільності |
Сума квадратів |
Середній квадрат |
Математичне сподівання середнього квадрату |
|
|
|
|
|
Залишок |
|
|
|
|
Загальна сума |
|
|
|
|
Якщо 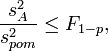 то
вплив фактора
слід
вважати незначним. При цьому загальна
дисперсія
то
вплив фактора
слід
вважати незначним. При цьому загальна
дисперсія ![]() пов’язана
тільки з фактором випадковості і може
служити оцінкою для дисперсії відтворення.
Така оцінка краща від
,
бо має більше число степенів вільності.
Якщо ж справедлива нерівність
пов’язана
тільки з фактором випадковості і може
служити оцінкою для дисперсії відтворення.
Така оцінка краща від
,
бо має більше число степенів вільності.
Якщо ж справедлива нерівність
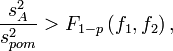 де
де ![]() та
та ![]() ,
різниця між дисперсіями
та
значна
і, відповідно, значний вплив фактора
.
,
різниця між дисперсіями
та
значна
і, відповідно, значний вплив фактора
.
