Лекция № 23 “Тригонометрические ряды. Ряды Фурье”

1. Гармонический анализ. Тригонометрический ряд.

В науке и технике довольно часто приходится иметь дело с периодическими явлениями. Такие явления через определенный промежуток времени , называемый периодом, возвращают систему в начальное состояние. Из материала Лекции № 12 Первого семестра известно, что периодической функцией называется функция, удовлетворяющая равенству . Простейшей периодической функцией является синусоида , где – амплитуда, – частота, – начальная фаза. Очевидно, что сложение синусоид с разными амплитудами и одинаковыми частотами и фазами приводит к той же синусоиде с увеличенной амплитудой. Сложение же синусоид, различающихся амплитудами, частотами и фазами приводит к периодической функции, вид которой отличается от синусоиды.

О1. Ряд вида

называется тригонометрическим рядом.

Из определения тригонометрического ряда видно, что периодическая функ

ция может быть представлена в виде суммы синусоид с различающими-ся амплитудами, частотами и фазами, т.е. может быть разложена на простые гармонические колебания.

О2. Отдельные составляющие функции называются гармоническими составляющими или гармониками, а процесс разложения периодической функции на гармоники называется гармоническим анализом.

Если в качестве независимой переменной выбрать величину , то функция также будет периодической функцией, но уже со стандартным периодом . Разложение этой функции в тригонометрический ряд имеет вид

.

Используя формулу и вводя обозначения , и , приведем тригонометрический ряд к виду .

2. Ряд Фурье.

Т1. Если функция определена и интегрируема на сегменте , разлагается в тригонометрический ряд

,

который равномерно сходится, то это разложение единственно.

Док-во. Интегрируя почленно тригонометрический ряд (это можно делать в силу его равномерной сходимости (см. Лекцию № 21)), получим

.

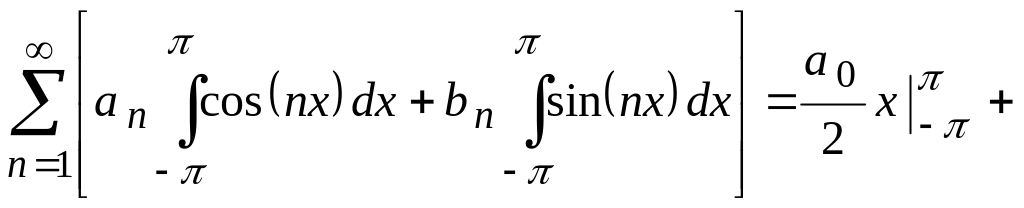
Откуда находим, что . Рассмотрим интегралы вида:

а) ; б) ; в) .

В случае :

а) (как интеграл от четной функции по симметричному интервалу интегрирования (см. Лекцию № 8))

.

б) (как интеграл от нечетной функции по симметричному интервалу интегрирования (см. Лекцию № 8). Этот интеграл равен нулю и в случае по той же причине).

в) (как интеграл от четной функции по симметричному ин-тервалу интегрирования (см. Лекцию № 8))

.

В случае :

а) (как интеграл от четной функции по симметричному интервалу интегрирования) .

в) (как интеграл от четной функции по симметричному интервалу интегрирования) .

Умножим тригонометрический ряд на и проинтегрируем его на отрезке , получим:

(с учетом полученных результатов) . Отсюда находим, что .

Умножим тригонометрический ряд на и проинтегрируем его на отрезке , получим:

(с учетом полученных результатов) . Отсюда находим, что .

Итак, коэффициенты тригонометрического ряда однозначно определяются формулами: ; ; . Следовательно, разложение функции в тригонометрический ряд единственно.

О3. Тригонометрический ряд с коэффициентами, определяемыми формулами: ; ; называется рядом Фурье.

Пример 1. Разложить в ряд Фурье функцию на сегменте .

Для того чтобы разложить в ряд Фурье функцию на сегменте , необходимо и достаточно вычислить коэффициенты этого ряда: ;

;

.

Следовательно, разложение в ряд Фурье функции имеет вид:

.

З1. Если функция периодична с периодом и разлагается в

ряд Фурье, то ее можно разложить на любом интервале длиной , например, , или .

Пример 2. Разложить в ряд Фурье функцию на сегменте .

Вычислим коэффициенты ряда Фурье

;

;

.

Таким образом, .