2. Свойства суммы функционального ряда.
1. Если все члены функционального ряда непрерывны на области определения и ряд равномерно сходится, то сумма ряда непрерывна в области определения .
2. Если все члены функционального ряда непрерывны на интервале и ряд равномерно сходится, то на этом интервале функциональный ряд можно почленно интегрировать, т.Е.
.
3.
Пусть на области определения
все члены функционального ряда
имеют
непрерывные производные и ряд
сходится
.
Если ряд, составленный из производных
равномерно сходится, то исходный ряд
равномерно сходится.
Пример
1.
Исследовать на сходимость ряд
.
Данный
функциональный ряд
представляет собой сумму бесконечной
геометрической прогрессии с первым
членом
и со знаменателем
.
Известно, что бесконечная геометрическая
прогрессия сходится при
,
т.е. функциональный ряд будет сходиться
при
.
Следовательно, функциональный ряд
сходится
,
причем равномерно, так как
.
Пример
2.
Вычислить сумму ряда
.
Если ряд равномерно сходится, то
проинтегрировать его.
Данный
ряд представляет собой сумму бесконечной
геометрической прогрессии с первым
членом
и со знаменателем
.
Известно, что бесконечная геометрическая
прогрессия сходится при
,
т.е. функциональный ряд будет сходиться
при
или
.
Следовательно, функциональный ряд
сходится, так как его сумма
.
Данный ряд может быть промажорирован
рядом
при
,
поэтому он сходится равномерно
.
Отсюда следует, что его можно почленно
проинтегрировать на интервале от
до
при
.
Тогда
.
Полученное
выражение представляет собой разложение
функции
в ряд Маклорена, который равномерно
сходится
при
.
Лекция № 22 “Степенные ряды”
1. Теорема Абеля. Радиус и интервал сходимости степенного ряда.
О1.
Ряд
(или
ряд более общего вида
,
где
)
называется степенным
рядом.
Так как степенной ряд являются частным случаем функционального ряда, то он характеризуется областью сходимости, для нахождения которой применяется теорема Абеля.
Т1.
Если степенной ряд сходится при
(
),
то он сходится абсолютно
,
удовлетворяющих неравенству
.
Если степенной ряд расходится при
(
),
то он расходится абсолютно
,
удовлетворяющих неравенству
.
Док-во.
Так как числовой ряд
сходится, то его общий член
при
,
т.е. последовательность
ограничена. Это означает, что существует
такое положительное число
,
что
выполняется неравенство
.
Перепишем степенной ряд в виде
и рассмотрим ряд составленный из модулей
членов этого ряда:
.
В
силу ограниченности каждого члена
числового ряда
имеем неравенство:
.
Ряд,
стоящий в круглых скобках, является
суммой бесконечной геометрической
прогрессии со знаменателем
,
которая имеет конечную сумму при
,
следовательно, при
исходный степенной ряд мажорируется
сходящимся рядом. По признаку сравнения
данный ряд сходится. Пусть теперь
существует такое число
,
для которого
и при котором исходный ряд сходится.
Так как бесконечная геометрическая
прогрессия имеет бесконечную сумму при
(
),
то степенной ряд расходится при
.
З1.
Теорема Абеля утверждает, что если
степенной ряд сходится в точке
(
),
то он абсолютно сходится во всех точках
интервала
(Рис.
22).
Рис. 22. Область сходимости степенного ряда.
Если
степенной ряд расходится в точке
(
),
то он абсолютно сходится во всех точках
интервала
(Рис.
23).
Рис.
23.
Область расходимости сте-
пенного ряда.
Отсюда вытекает теорема об интервале сходимости степенного ряда.
Т2.
Если степенной ряд
сходится не при всех значениях величины
и не только при
,
то существует число
такое, что степенной ряд абсолютно
сходится при
и расходится при
.
О2.
Число
называется радиусом
сходимости
степенного ряда, а интервал
– интервалом
сходимости.
Рассмотрим теорему, которая дает алгоритм поиска радиуса сходимости .
Т3.
Если существует предел
,
то радиус сходимости
степенного ряда
равен
.
Док-во.
Рассмотрим ряд
,
составленный из модулей членов степенного
ряда. По условию теоремы
.
Обозначим значение этого предела через
.
Тогда
.
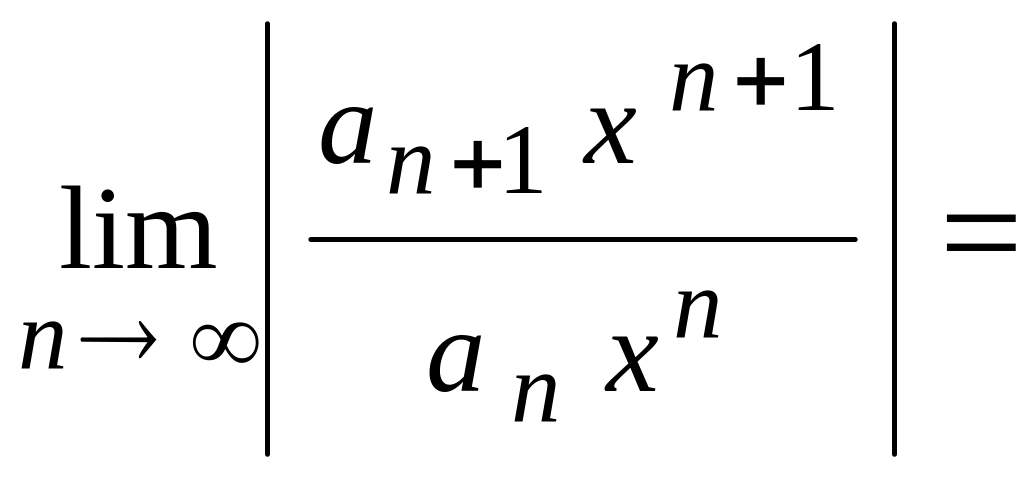
При каждом значении
степенной ряд становится числовым. По
признаку Даламбера ряд с фиксированным
значением величины
будет сходиться при выполнении неравенства
,
т.е. при
.
Следовательно, степенной ряд сходится
абсолютно при
и расходится при
для всех
по признаку Даламбера.
З2.
Если
,
то радиус сходимости
,
т.е. степенной ряд сходится на всей
числовой оси. Если
,
то радиус сходимости
,
т.е. степенной ряд сходится в единственной
точке
.
Пример
1.
Найти радиусы и интервалы сходимости
рядов а)
;
б)
;
в)
.
а)
Коэффициент
,
следовательно,
.
Отсюда
,
таким
образом, интервал сходимости равен
.
б)
Коэффициент
,
следовательно,
.
Отсюда
,
таким образом, степенной ряд сходится на всей числовой оси.
в)
Коэффициент
,
следовательно,
.
Отсюда
,
таким образом, степенной ряд сходится только в точке .