2. Признак Даламбера.

Т2. Пусть для положительного ряда существует предел . Тогда при ряд сходится; при ряд расходится, а при признак Даламбера не работает.

Док-во. Пусть . Выберем число такое, чтобы выполнялось двойное неравенство . Так как при отношение , а величина , то существует такой номер , что будет выполняться неравенство , т.е. ; ; ; …; . В силу этих неравенств, начиная с номера каждый член ряда будет меньше каждого члена ряда , который сходится, так как , и представляет собой сумму бесконечной геометрической прогрессии

( ). Следовательно, по признаку сравнения ряд сходится. Аналогично доказывается случай, когда (доказать самостоятельно).

Пример 2. Исследовать на сходимость ряд .

Очевидно, что необходимый признак сходимости ряда выполняется, т.е. ряд подозрителен на сходимость. Применим признак Даламбера:

,

следовательно, заданный ряд сходится.

3. Интегральный признак Коши.

Если для ряда в выражении общего члена заменить дискретную переменную на непрерывный аргумент , то получим функцию .

Т3. Пусть функция удовлетворяет следующим требованиям:

– определена на луче ;

– непрерывна, положительна и монотонно убывает в области определения.

Тогда, если сходится несобственный интеграл I рода , то сходится и ряд , а в случае расходимости несобственного интеграла I рода – расходится и ряд .

Док-во. Изобразим графически функцию (Рис. 21):

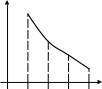
Рис. 21. Непрерывная функция, отображающая

числовой ряд.

. . .

Так как функция монотонно убывает, то для любого и справедливы неравенства . Проинтегрируем эти неравенства . В силу того, что и , то вводя обозначение , перепишем неравенство в виде . Составим для ряда -ую частичную сумму

.

Если интеграл сходится, то является конечным числом, а по признаку сравнения будет сходиться и ряд , в противном случае, когда , интеграл расходится, следовательно, будет расходиться и ряд .

Пример 3. Исследовать на сходимость ряд , если .

Так как , то введем в рассмотрение определенную и непрерывно убывающую на луче функцию и вычислим несобственный интеграл I рода при : . Отсюда видно, что

– при предел будет равен , т.е. интеграл расходится, следовательно, и данный ряд тоже расходится;

– при предел равен , т.е. интеграл сходится, следовательно, и данный ряд тоже сходится.

Рассмотрим случай, когда , т.е. исследуем на сходимость ряд .

О2. Ряд называется гармоническим рядом, а ряд – обобщенным гармоническим рядом.

Так как , то введем в рассмотрение определенную и непрерывно убывающую на луче функцию и вычислим несобственный ин-теграл I рода: . Отсюда видно, что по интегральному признаку Коши гармонический ряд расходится.