3. Понятие о неберущихся интегралах.

О1. Интегралы, первообразные для которых не выражаются через элементарные функции, называются неберущимися.

Пример 6. Приведенные интегралы являются неберущимися

.

Следующие интегралы вычислить самостоятельно, используя теоретический материал рассмотренной темы:

Пример 7. ; ; ; ;

; ; .

Тема: Определенный интеграл Лекция № 7 “Определенный интеграл и его свойства”

1. Задачи, приводящие к понятию определенного интеграла.

Задача 1. Пусть на сегменте задана непрерывная функция , график которой лежит выше оси абсцисс. Необходимо вычислить площадь криволинейной трапеции , ограниченной слева прямой , справа – прямой , снизу – прямой , а сверху – кривой . Из школьного курса математики известно, что в случае, когда на сегменте функция , то площадь прямоугольника (см. рис. а)) определяется по формуле (Рис. 5):

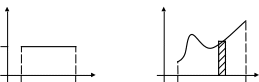а) б)

Рис. 5. Вычисление площади криволинейной трапеции.

Если на сегменте функция (см. рис. б)), для вычисления пло-щади криволинейной трапеции поступим следующим образом:

– сегмент произвольными точками разобъем на частей, т.е.

;

– внутри каждого элементарного сегмента возьмем произвольную точку и вычислим значение функции в этой точке;

– вычислим площадь элементарного прямоугольника , где ;

– просуммируем площади элементарных прямоугольников, получим прибли-

женное значение площади криволинейной трапеции

;

О1. Сумма называется интегральной суммой.

– обозначим через наибольшую длину элементарного сегмента и устремим количество точек разбиения к бесконечности, а величину , тогда получим точное значение площади криволинейной трапеции

.

Задача 2. Пусть материальная точка движется со скоростью . Требуется вычислить путь, пройденный точкой за время от до . Проводя аналогичные рассуждения, как и для задачи 1, получим .

Обобщая рассмотренные задачи, приходим к понятию определенного инте-грала.

О2. Пусть функция непрерывна на сегменте . Произведем следующие действия:

– сегмент произвольными точками разобъем на частей, т.е.

,

длину каждой части обозначим через ;

– внутри каждого элементарного сегмента возьмем произвольную точку и вычислим значение функции в этой точке;

– вычислим произведения ;

– просуммируем все проризведения предыдущего пункта, получим

;

– обозначим через наибольшую длину элементарного сегмента и устремим количество точек разбиения к бесконечности, а величину , тогда получим .

Если полученный предел существует, то он называется определенным интегралом от функции в пределах от до , т.е. , где число называется нижним, а число – верхним пределами интегрирования.

З1. В отличие от неопределенного интеграла, кототрый является функцией, определенный интеграл дает число.

О3. Функция называется интегрируемой на сегменте , если существует предел интегральной суммы.

З2. Если функция непрерывна на сегменте , то на этом сегменте она интегрируема.

С геометрической точки зрения определенный интеграл дает площадь криволинейной трапеции, а с физической точки зрения – путь, пройденный материальной точкой за данный промежуток времени.