2. Интегралы вида ( и – целые числа).
а)
Если хотя бы одно из чисел
или
является нечетным целым числом, то от
нечетной степени отделяют один множитель,
а оставшуюся четную часть выражают
через другую тригонометрическую функцию
с помощью основного тригонометрического
тождества
,
при этом надо помнить, что
,
а
.
Пример 2.
Вычислить
.
Согласно изложенному способу вычисления, получим
.
Пример 3.
Вычислить
.
.
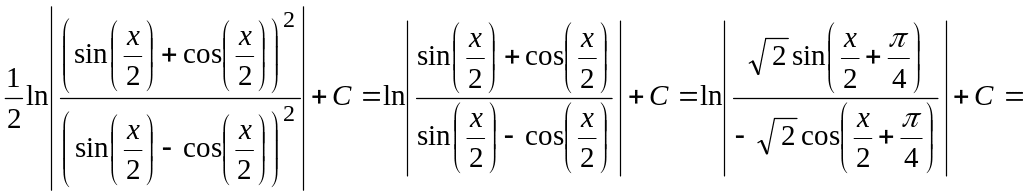
Пример 3.
Вычислить
(самостоятельно).
б) Если и являются четными неотрицательными целыми числами, то используют тригонометрические формулы понижения степени
формулы подобия, например,
,
…
Пример 4.
Вычислить
.
.
3. Интегралы вида , , .
При вычислении таких интегралов используют формулы:
;
;
и
формулы подобия:
,
,
...
Пример 5.
Вычислить
.
Так как
и
(обратите
внимание на тот факт, что величина
всегда определяется по синусу при
наличии косинуса), то
.
Пример 6.
Вычислить
.
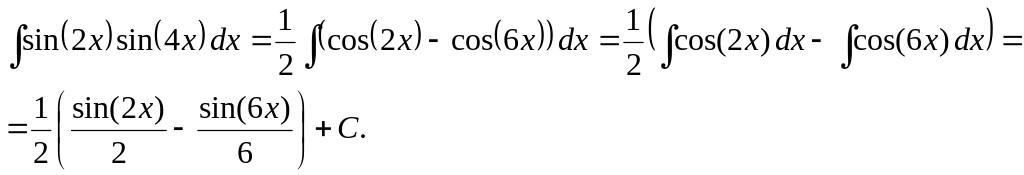
4. Интегралы вида и
( и – целые положительные числа).
Напомним,
что
,
,
,
.
При интегрировании используются формулы
;
,
при этом надо помнить, что
и
.
Пример 7.
Вычислить
.
Преобразуем подинтегральную функцию к виду
.
Частными
случаями рассмотренных интегралов
являются интегралы
и
(
).
Такие интегралы вычисляются путем
отделения квадрата подинтегральной
функции и использованием вышеприведенных
формул.
Пример 8.
Вычислить
.
.
5. Интегралы вида и
( – целое положительное число).
Такие интегралы вычисляются по частям с использованием рекуррентных формул. Вычислим, например,
.
Решая это равенство
относительно величины
,
получаем
.
О1. Соотношения полученного типа называются рекуррентными.
Рекуррентные соотношения позволяют по известному значению более низкого порядка вычислять значения искомой величины более высокого порядка. Аналогично полученному рекуррентному соотношению получают формулу для вычисления .
Пример 9.
Вычислить
.
Согласно рекуррентному соотношению получаем
.
Интеграл
вычислен в п. 2а), поэтому окончательный
ответ имеет вид
.
Лекция № 6 “Интегрирование некоторых иррациональных функций”
1. Интегралы вида .
Интегралы такого типа вычисляются по следующей схеме:
– у
дробей
находят наименьший общий знаменатель,
который обозначим через
;
– проводят
замену
.
В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.
Пример 1.
Вычислить
.
В данном примере
,
следовательно, наименьший общий
знаменатель этих дробей равен 6. Таким
образом,
.
2. Интегралы вида .
Такие интегралы
путем замены
приводятся к одному из интегралов
вида:
1.
;
2.
;
3.
.
Для вычисления
этих интегралов применяют следующие
тригонометрические замены 1.
;
2.
;
3.
–
которые позволяют избавиться от
квадратного корня.
Пример 2.
Вычислить
.
Данный интеграл соответствует интегралам типа 1., поэтому
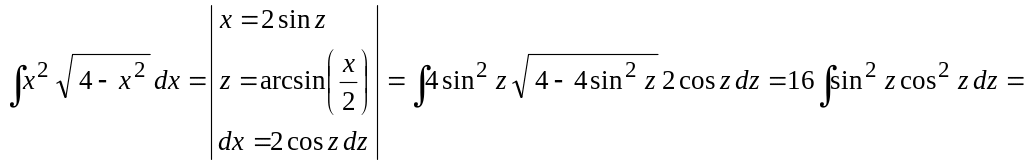(этот интеграл
вычислен в Лекции
№ 5,
см. Пример 4)
.
Пример 3.
Вычислить
.
Воспользуемся указанной выше заменой
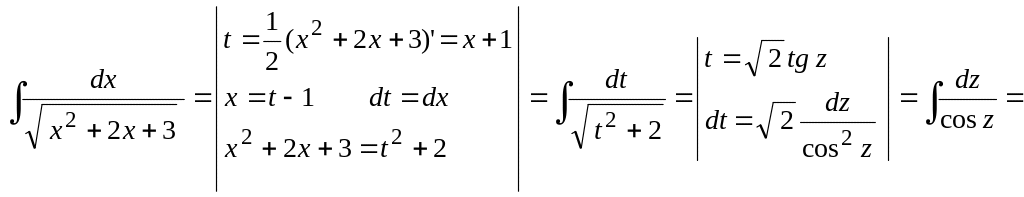
(интеграл вычислен
в п. 2а)
.
Пример 4.
Вычислить
.
.
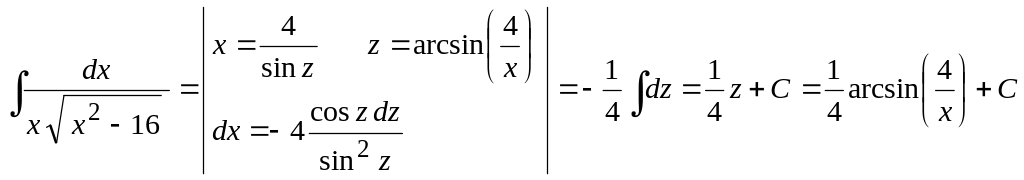Пример 5.
Вычислить
.
Воспользуемся указанной выше заменой
.
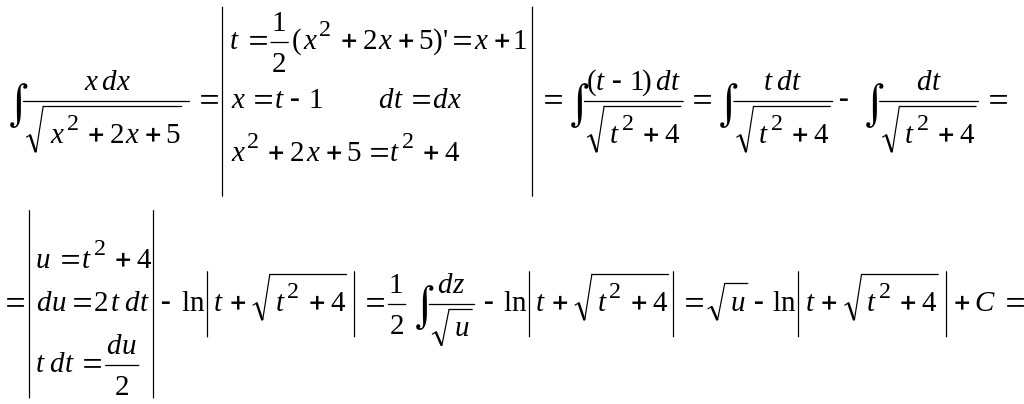