5. Сумма простых дробей приводится к общему знаменателю и числитель получившейся дроби приравнивается к числителю исходной дроби

или

или после раскрытия скобок и приведения подобных членов получаем

6. Сравнивая коэффициенты при одинаковых степенях переменной величины в левой и правой частях равенства, получают систему линейных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов :

З5. Если разложение полинома, стоящего в знаменателе дроби, на простые множители содержит не кратные действительные корни, то процедура отыскания неопределенных коэффициентов может быть упрощена путем подстановки в левую и правую части равенства значений корней, например,

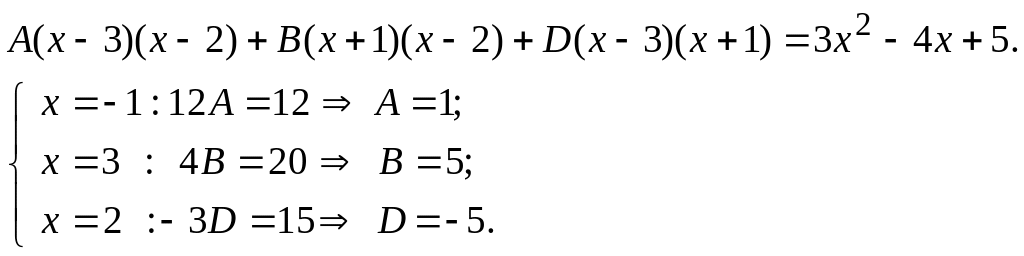
7. Решают слау и находят числовые значения неизвестных коэф-фициентов

Для рассматриваемого примера .

8. Числовые значения неопределенных коэффициентов подставляют в разложение правильной рациональной дроби на простые дроби (п.4 данной схемы) .

9. Полученное разложение рациональной дроби на простые дроби ин-тегрируется .

Пример 6. Вычислить .

Подинтегральная функция представляет собой неправильную рациональную дробь, поэтому выделим “целую” часть и правильную рациональную дробь:

.

Разложив знаменатель правильной рациональной дроби на простые множители, представим эту дробь в виде суммы простых дробей:

.

Приводя сумму простых дробей к общему знаменателю и приравнивая числитель получившейся дроби к числителю исходной дроби, получим после раскрытия скобок и приведения подобных членов:

.

Сравнивая коэффициенты при одинаковых степенях , получаем СЛАУ:

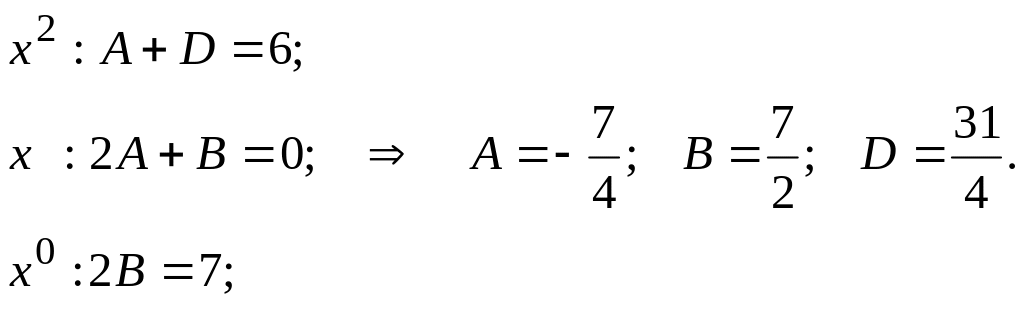
Таким образом, подинтегральную функцию можно представить в виде:

.

Проинтегрируем полученное выражение

.

Интегрирование последней дроби рассмотрено ниже.

3. Интегрирование простых дробей.

При интегрировании рациональных дробей возникают интегралы вида и с квадратичным полиномом, имеющим отрицатель-ный дискриминант . Интегралы первого вида путем замены сводятся к табличным интегралам . Интегралы второго вида вычисляются с помощью замены , которая приводит к интегралу 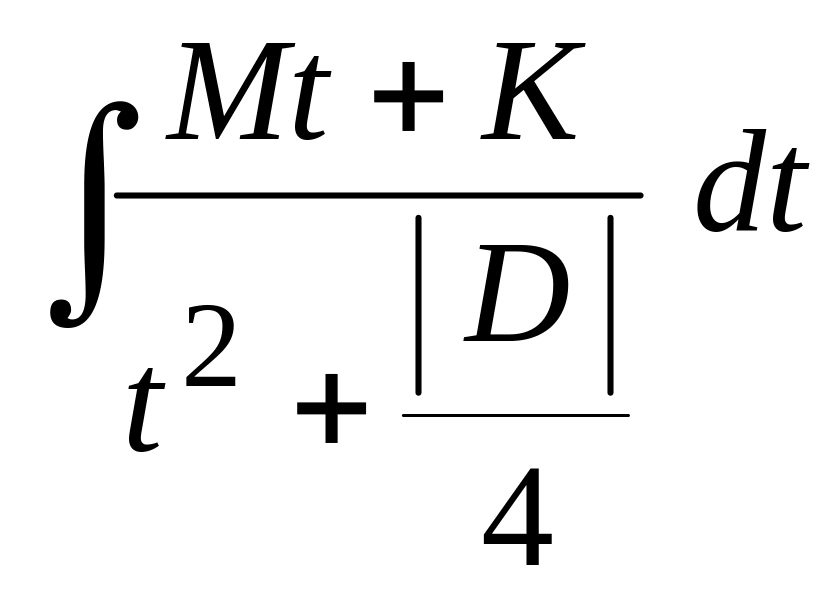, где . Использование метода тождественных преобразований подинтегральной функции позволяет записать этот интеграл в виде:

.

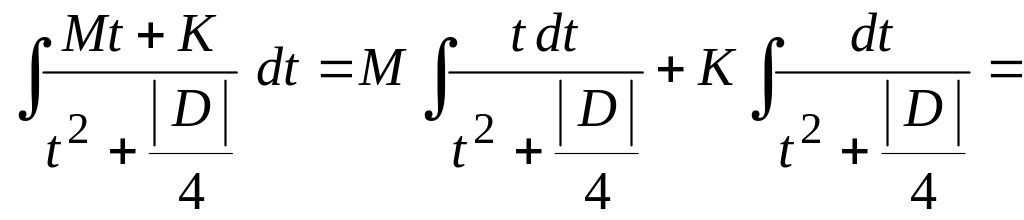
Пример 7. Вычислить .

Воспользуемся указанной выше заменой

.

Лекция № 5 “Интегрирование тригонометрических функций”

1. Универсальная тригонометрическая подстановка.

При вычислении неопределенных интегралов от рациональной функции, зависящей только от тригонометрических функций применяется универсальная тригонометрическая подстановка, применение которой обосновано следующими формулами, связывающими функции синуса и косинуса с тангенсом половинного аргумента

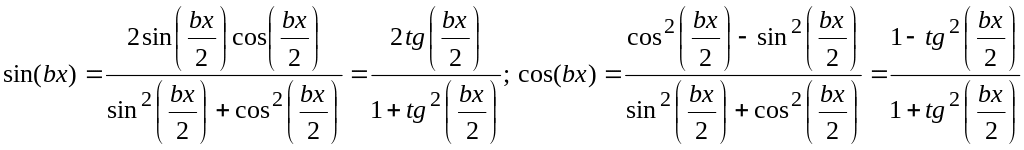
При вычислении проводят универсальную тригонометрическую подстановку 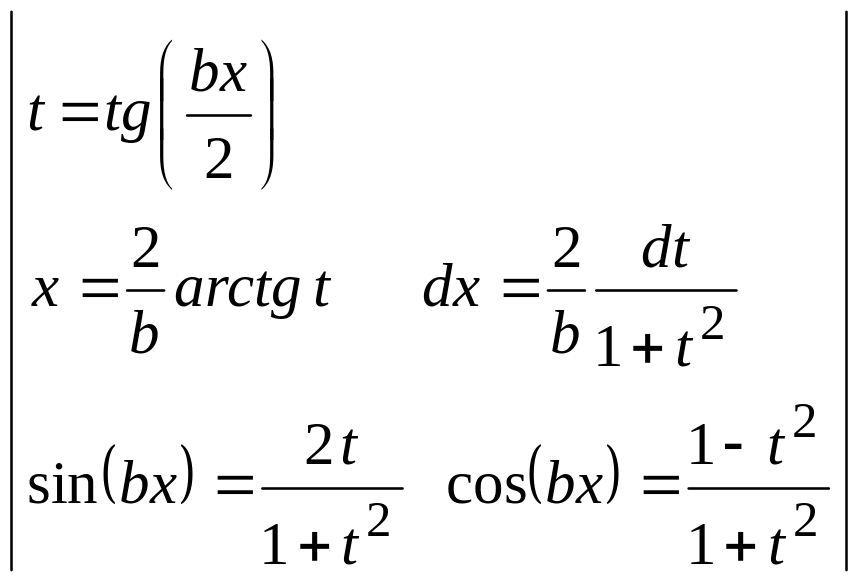. Из этих формул видно, что вне зависимости от величины параметра формулы для синуса и косинуса носят универсальный характер.

Пример 1. Вычислить .

Воспользуемся универсальной тригонометрической подстановкой

.

З1. Отметим, что универсальную тригонометрическую подстановку следует применять не во всех случаях. Для некоторых типов интегралов от тригономнтрических функций, которые будут рассмотрены ниже, существуют более простые способы вычисления.