4. Нестандартные интегралы требуют для своего вычисления приобретения опыта на практических занятиях.

Пример 16. Найти .

.

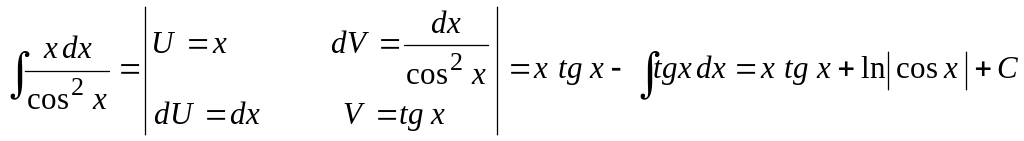
Лекция № 3 “Комплексные числа”

1. Формы записи комплексного числа.

Решение простейшего квадратного уравнения невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим .

О1. Выражение называется мнимой единицей.

О2. Комплексным числом называется выражение вида , где – вещественные числа, причем называется действительной, а – мнимой частями комплексного числа .

О3. Приведенная форма записи комплексного числа называется алгеб-раической.

О4. Два комплексных числа и называются равными, если равны их вещественные и мнимые части, т.е. и .

О5. Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.

О6. Комплексно-сопряженным к комплексному числу называ-ется комплексное число .

Пример 1. Записать комплексно-сопряженное число к комплексному числу

.

Согласно определению комплексно-сопряженного числа получаем .

З1. Двойное комплексное сопряжение приводит к исходному комплексному числу, т.е. .

Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.

Пример 2. Решить квадратное уравнение .

Вычислим дискриминант уравнения , таким об-разом, . Следовательно, и .

З2. Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.

Комплексное число изображается на комплексной плоскости в виде вектора, соединяющего начало координат с точкой (Рис. 2):

Рис. 2. Изображение комплексного числа на комплексной

плоскости.

Пример 3. Изобразить на комплексной плоскости число (Рис. 3).

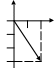
2

Рис. 3. Изображение комплексного числа на

комплексной плоскости.

- 3

Если перейти от декартовой системы координат к полярной системе отсчета, т.е. ( ), то комплексное число .

О7. Полученная форма записи комплексного числа называется тригонометрической.

Обратный переход от полярной системы отсчета к декартовой системе коор-динат осуществляется по формулам: , при этом является модулем, а – аргументом комплексного числа .

З3. Аргумент комплексного числа определяется в зависимости от знаков вещественной и мнимой частей: .

2. Действия с комплексными числами.

1. Для того чтобы сложить (найти разность) два комплексных числа и , надо сложить (найти разность) отдельно действительные и мнимые части, т.е. .

Пример 4. Найти сумму и разность чисел и . Изобразить все числа на комплексной плоскости.

Найдем сумму заданных комплексных чисел . Вычислим разность данных чисел . Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):

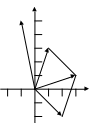
Рис. 4. Изображение комплексных чисел

. на комплексной плоскости.

З4. Отметим, что , а .

2. Для того чтобы найти произведение двух комплексных чисел и , надо их перемножить, как два выражения с учетом того, что : .

З5. Отметим, что .

З6. Произведение комплексных чисел в тригонометрической форме записи имеет вид

Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, -ая степень любого комплексного числа будет иметь вид . При извлечении корня -ой степени применяют формулу Муавра

,

где величина .

3. Деление комплексного числа на комплексное число осуществляется так .

З7. Деление комплексных чисел в тригонометрической форме записи имеет вид , т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.