3. Таблица основных неопределенных интегралов.

Подинтегральная функция	Неопределенный интеграл	Частные случаи
Степенная
Показательная
Тригонометрические

Пример 3. Используя таблицу неопределенных интегралов, вычислить интегралы (самостоятельно).

Лекция № 2 “Методы интегрирования”

1. Метод тождественных преобразований подинтегральной функции.

Данный метод основан на использовании простых приемов, алгебраических и тригонометрических формул, свойств подинтегральной функции, разложения полиномов на простые множители и свойств неопределенного интеграла. Рассмотрим этот метод на конкретных примерах.

1. Почленное деление числителя дроби на ее знаменатель .

З1. Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е. .

Пример 1. Найти .

Выполним в подинтегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла

.

З2. Из этого примера видно, что слова “найти неопределенный интеграл” означают за счет преобразований подинтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.

33. Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования пишется один раз, так сумма или разность постоянных интегрирования все равно есть постоянная величина.

2. Использование противоположных арифметических операций (например, сложение-вычитание).

Пример 2. Найти .

Анализ подинтегральной функции показывает, что в числитель дроби надо добавить и вычесть 1 (при этом подинтегральная функция не изменится), а затем воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)

.

3. Использование алгебраических и тригонометрических формул, например,

и других формул.

Пример 3. Найти .

Воспользуемся формулой квадрата разности

.

Пример 4. Найти .

Поступим аналогично примеру 3

.

4. Использование свойств функций, например,

.

Пример 5. Вычислить .

.

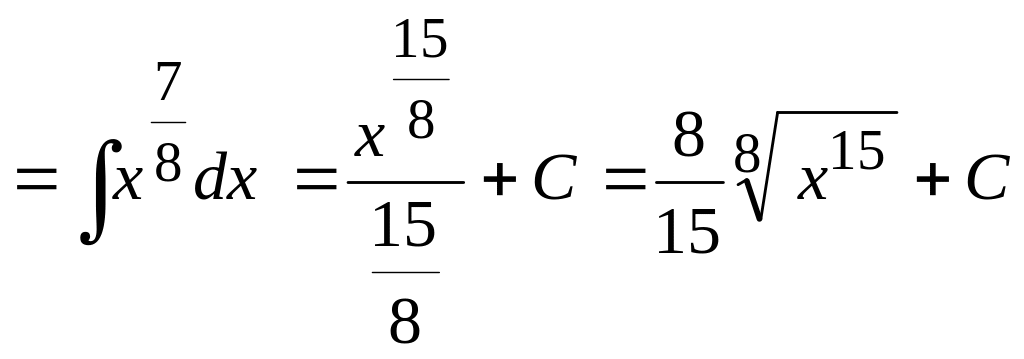Пример 6. Вычислить .

.

5. Использование разложения полиномов на простые множители, например, , где и корни уравнения .

Пример 7. Найти .

По теореме Виета уравнение имеет корни и , сле-довательно, разложение квадратичного полинома на простые множители имеет вид: . Подставим полученное выражение в под-интегральную функцию, получим

.