2. Принцип суперпозиции частных решений.
При решении ЛНДУII с постоянными коэффициентами полезной может оказаться теорема, определяющая принцип суперпозиции частных решений.
Т1. Частное решение ЛНДУ II с постоянными коэффициентами вида
ищется
в виде суперпозиции частных решений
,
которые являются частными решениями
уравнений
.
Пример
3.
Решить ДУ II
.
Согласно
изложенной методике найдем решение
однородного уравнения, которое ищем в
виде
,
тогда
.
Следовательно,
характеристическое уравнение имеет
вид
.
Корни уравнения в этом случае вещественные
и равны
,
следовательно, два частных линейно-независимых
решения однородного ДУ II имеют вид
и
.
Тогда общее решение ЛОДУ II
с постоянными коэффициентами в данном
случае будет иметь вид:
.
Проанализируем
правую
часть данного ЛНДУ II,
которая состоит из суммы двух функций,
первая из которых равна
,
а вторая
.
Согласно принципу суперпозиции частных
решений частное решение данного ЛНДУ
II
будем искать в виде
,
причем первое частное решение удовлетворяет
уравнению
,
а второе частное решение – уравнению
.
Решим первое уравнение приведя ее правую
часть к теоретическому виду:
,
т.е.
,
а
.
Следовательно, комплексное число
,
поэтому частное решение неоднородного
дифференциального уравнения ищем в
виде
.
Найдем
первую и вторую производные этой функции
и подставим найденные функции в исходное
уравнение
или
.
Сравнивая коэффициенты при одинаковых
фун-кциях находим
.
Решаем эту систему и определяем
неизвестные коэффициенты:
,
а коэффициент
.
Таким образом, частное решение
неоднородного ДУII
имеет вид:
.
Решим второе уравнение, приведя правую
часть данного ЛНДУII
к теоретическому виду:
.
Следовательно,
,
поэтому частное решение неоднородного
дифференциального уравнения ищем в
виде
.
Найдем первую и вторую производные этой
функции и подставим найденные функции
в исходное уравнение
.
Сравнивая коэффициенты при одинаковых степенях аргумента находим
.
Решаем эту систему и определяем
неизвестные коэффициенты:
,
а коэффициент
.
Таким образом, частное решение
неоднородного ДУII
имеет вид:
.
Общее решение исходного неоднородного
ДУII
определяется суммой всех найденных
функций
.
Лекция № 17 “Применение ду II к изучению механических и электрических колебаний”
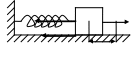
1. Колебания тела на пружине.
Пусть тело массой
прикреплено к пружине с коэффициентом
упругости
,
коэффициент трения о горизонтальную
плоскость равен
.
Выведем тело из положения равновесия
и отпустим. На тело действуют следующие
силы: сила упругости
,
сила трения
и внешняя вы-нуждающая сила
,
которая является равнодействующей всех
внешних сил, действующих на тело (Рис.
19):
Рис.
19. Колебание
тела на пружине.
По второму закону
Ньютона
,
где
– уско-рение, следовательно, уравнение
движения имеет вид
.
Введя обозначения
,
и
,
перепишем полученное уравнение в виде
.
Это уравнение описывает колебания с
трением под действием внешней силы.
Рассмотрим частные случаи этого
уравнения:
1). Пусть отсутствуют
внешние силы (
)
и сила трения (
),
тогда уравнение принимает вид
и описывает
свободные колебания.
С математической точки зрения данное
уравнение является линейным однородным
дифференциальным уравнением второго
порядка, поэтому ищем его решение в виде
.
В этом случае характеристическое
уравнение определяется квадратным
уравнением вида
,
корнями которого будут величины
.
Следовательно, общее решение
.
Преобразуем это равенство следующим образом
.
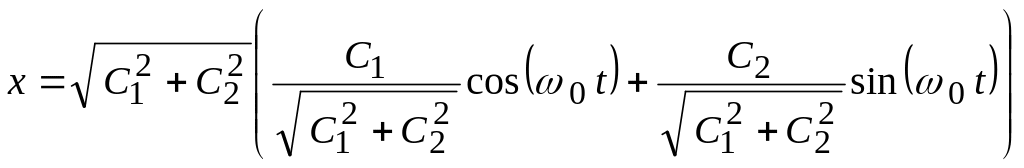Вводя обозначения
,
и
,
получим формулу, описывающую свободные
колебания
,
где
– амплитуда колебаний,
– фаза колебаний,
– начальная фаза колебаний.
2). Пусть отсутствуют
внешние силы (
),
т.е. колебания
осуществляются с трением (диссипативная
система).
В этом случае уравнение колебаний имеет
вид
,
а характеристическое уравнение дается
квадратным уравнением
.
С практической точки зрения наибольший
интерес представляет случай, когда
.
В этом случае корни характеристического
уравнения равны
,
где
.
Проводя преобразования аналогичные
тем, которые были проведены для предыдущего
случая, запишем формулу, описывающую
затухающие колебания
.
Из формулы видно, что при наличии силы
трения колебания происходят с уменьшающейся
амплитудой при увеличении времени
.
3). Пусть отсутствует
сила трения (
),
т.е. колебания
осуществляются под действием внешних
сил,
тогда уравнение принимает вид
.
Если внешняя сила описывается периодической
функцией
,
то решение ЛНДУ II
представляется в виде суммы решения
однородного ДУ II
(см. случай 1)
и частного решения неоднородного ДУ
II,
которое будем искать в виде
.
а)
пусть
(
),
тогда
.
Подставляя эту функцию и ее вторую
производную в уравнение, сравнивая
коэффициенты при одинаковых функциях
и решая систему линейных алгебраических
уравнений относительно неизвестных
коэффициентов
и
,
получаем, что
,
а
,
следовательно, общее решение имеет вид
;
)
пусть
,
но
и
,
тогда решение принимает вид
;
)
пусть
и
,
тогда
.
б)
пусть
(
),
тогда
.
Подставляя эту функцию и ее вторую
производную в уравнение, сравнивая
коэффициенты при одинаковых функциях
и решая систему линейных алгебраических
уравнений относительно неизвестных
коэффициентов
и
,
получаем, что
,
,
следовательно, общее решение имеет вид
(решение дифференциальных уравнений в случаях а) и б) провести самостоятельно).