Тема: Неопределенный интеграл

(О – определение; З – замечание; Т – теорема; Док-во – доказательство, Сл – следствие.)

Лекция № 1 “Неопределенный интеграл и его свойства”

1. Первообразная. Неопределенный интеграл.

При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.

О1. Первообразной функции называется такая функция , первая производная от которой равна заданной функции, т.е. .

Т1. (о существовании первообразной) Если функция непрерывна на сегменте , то на этом интервале существует первообразная этой функции.

Т2. Если – первообразная функции , то функция ( – произвольная постоянная) также является первообразной функции .

Док-во. .

Т3. Если и первообразные функции , то они отличаются друг от друга на постоянную величину.

Док-во. Пусть и . Введем в рассмотрение вспомога-тельную функцию и рассмотрим эту функцию на открытом интервале . По теореме Лагранжа для любого интервала выполняется равенство , где . По условию теоремы , следовательно, В силу произвольности точек и полученное равенство выполняется для всего исследуемого интервала. Это означает, что , откуда и вытекает утверждение теоремы.

Пример 1. Пусть дана функция . Найти первообразную этой функции. В случае наличия двух первообразных показать, что они отличаются на постоянную величину.

Для функции существуют две первообразные и . Их разность .

О2. Совокупность всех первообразных функции называется неопределенным интегралом и обозначается , где – переменная интегрирования, – подинтегральная функция, – подинтегральное выражение.

На основании Т2 и Т3 можно записать, что .

О3. Отыскание всех первообразных называется неопределенным интегрированием.

Выясним геометрический смысл неопределенного интеграла. Пусть дана функция и требуется найти такую кривую , для которой в каждой ее точке тангенс угла наклона касательной равен значению функции в этой точке. Такой линией будет кривая, для которой . Таким образом, неопределенный интеграл определяет все кривые, у которых тангенс угла наклона в каждой ее точке совпадает со значением функции .

Пример 2. Построить кривые, которые задаются неопределенным интегралом .

Первообразной для подинтегральной функции будет функция , следовательно, . Построим эти кривые (Рис. 1):

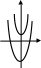
Рис. 1. Интегральные кривые .

2. Свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подинтегральной функции .

Док-во. По определению неопределенного интеграла

.

2. Дифференциал неопределенного интеграла равен подинтегральному выражению .

Док-во. По определению дифференциала от неопределенного интеграла имеем

.

3. Если подинтегральное выражение является дифференциалом некоторой функции , то неопределенный интеграл равен .

Док-во. Так как , то .

4. Неопределенный интеграл от линейной комбинации функций равен той же самой линейной комбинации неопределенных интегралов от этих функций .

Частные случаи:

а) неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций

.

б) постоянный множитель можно выносить за знак неопределенного интеграла .

5. Формула неопределенного интеграла не зависит от обозначения пере-

менной интегрирования .