2. Дуi с разделяющимися переменными.
О12. Дифференциальное
уравнение вида
называется
ДУI
с разделяющимися переменными.
Решение ДУI с разделяющимися переменными решают по схеме:
– обе
части уравнения умножают на
,
при этом уравнение принимает вид
;
– обе
части уравнения делят на функцию
,
т.е. приводят уравнение к виду
(точки,
в которых
определяют особые точки, при этом
получаемые решения являются особыми);
О13. Дифференциальное
уравнение вида
называется
ДУI
с разделенными переменными.
– ДУI
с разделенными переменными интегрируется,
т.е.
.
З3. В общем случае ДУI с разделяющимися переменными имеет вид:
.
Деля ДУI
на произведение
,
получаем дифференциальное уравнение
с разделенными переменными
.
Особые решения данного ДУI
следуют из решения уравнений
и
.
ДУI
с разделенными переменными интегрируют
.
Пример 3.
Решить ДУI
.
Разделим все
уравнение на произведение функций
(особой точкой является точка
),
получим
.
Полученное ДУ I
с разделенными переменными интегрируем
.
Вычислим неопре-деленные интегралы,
получим общее решение данного ДУ I
.
Лекция № 13 “Однородные и линейные ду I”
1. Однородные ду I.
О1.
Функция
называется
однородной
функцией
-го
измерения
относительно
переменных
и
,
если
имеет место равенство
.
Пример
1.
Однородны ли функции
и
?
Используя определение однородной функции, получаем
– однородная функция второго измерения;
– однородная функция нулевого измерения .
Рассмотрим
ДУ I
,
где
– однородная функция. Выберем
,
тогда дифференциальное уравнение
запишется в виде
.
З1.
Если правая часть ДУ I
зависит только от отношения
,
то это однородное ДУ I.
Решение однородного ДУ I проводится по схеме:
–
вводят
новую функцию
;
–
находят
производную
;
–
найденные
величины подставляют в однородное ДУ
I
;
З2. В результате указанной замены однородное ДУ I сводится к ДУ I с разделяющимися переменными.
– решают ДУ I с разделяющимися переменными:
;
;
;
;
;
–
находят
искомую функцию
.
Пример
2.
Решить ДУ I
.
В
правой части разделим числитель и
знаменатель дроби на
,
получим
уравнение
,
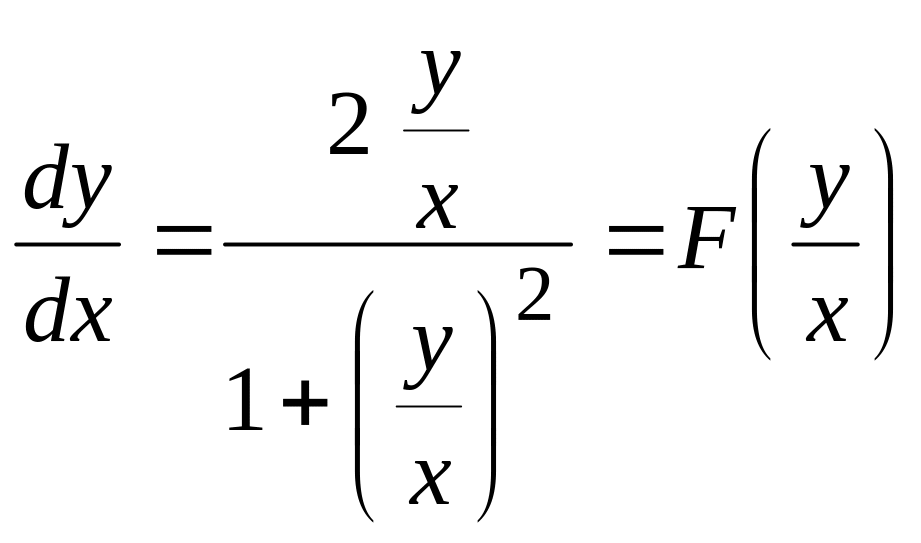следовательно, данное дифференциальное
уравнение первого порядка является
однородным. Будем действовать в
соответствии со схемой решения:
;
;
;
;
;
;
;
.
Для вычисления интеграла применим метод тождественных преобразований подинтегральной функции (см. Лекцию № 2)
.
З3.
Если
искомая функция и ее аргумент входят в
полученное общее решение дифференциального
уравнения под знаком логарифма, то
постоянную интегрирования рекомендуется
выбирать в виде
.
В общем случае постоянная интегрирования
выбирается из соображений упрощения
формы записи общего решения дифференциального
уравнения.
С учетом замечания и определения функции получаем
;
;
.
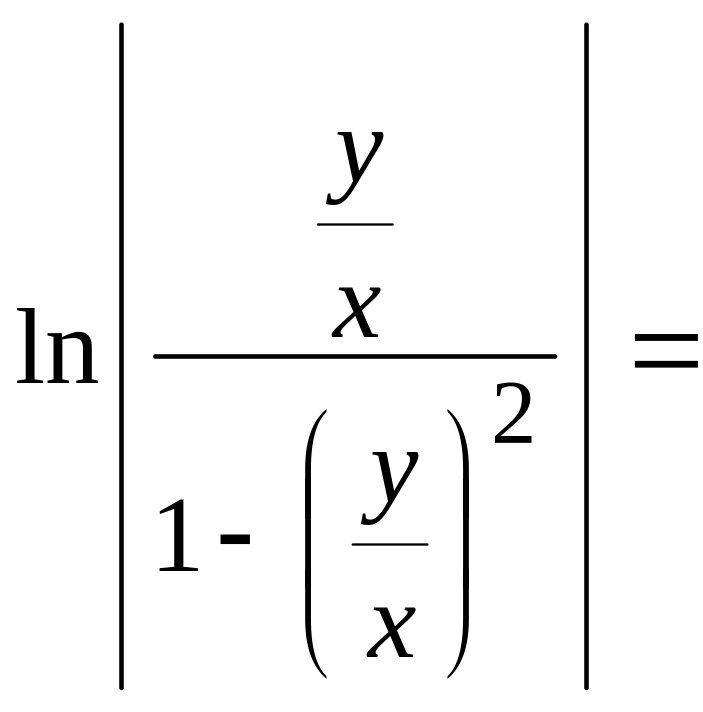
Потенцируя
полученное равенство и сокращая обе
части равенства на
,
получим общее решение заданного
однородного дифференциального уравнения
.
З4.
Если однородное ДУ I
задано в дифференциалах
,
то его преобразуют к виду
и решают по вышеприведенной схеме.
Пример
3.
Решить ДУ I
.
Приведем
заданное уравнение к обычному виду
.
В правой части разделим числитель и
знаменатель дроби на
,
получим уравнение
,
следовательно, данное дифференциальное
уравнение первого порядка является
однородным. Будем действовать в
соответствии со схемой решения:
;
;
;
;
;
;
;
.
Потенцируя полученное равенство и
умножая обе части равенства на
,
получим общее решение заданного
однородного дифференциального уравнения
.