8.Емкость в цепи переменного тока. Рис. 2.12
Зададим изменение тока в емкости по синусоидальному закону
i(t) = ImC sin(ωt + ψi).
Используем уравнением связи между током и напряжением в емкости
uC = 1 / C · ∫ i dt,
и получим
uC = 1 / (ωC) · ImC (-cos(ωt + ψi)).
Заменим –cos на sin
(2.23) uC = 1 / (ωC) · ImC sin(ωt + ψi - 90°).
Формальная запись синусоидального напряжения имеет вид
(2.24) uC = UmC sin(ωt + ψu).
Соотношения (2.23) и (2.24) будут равны если выполняется условие равенства амплитуд и фаз
(2.25) UmC = 1 / (ωC) · ImC,
(2.26) ψu = ψi - 90°.
Уравнение (2.25) можно переписать для действующих значений (2.27) UC = 1 / (ωC) · IC.
Уравнение (2.26) показывает, что фаза напряжения в емкости отстает от фазы тока на 90°. Величину XC = 1 / (ωC) в уравнении (2.25) называют емкостным сопротивлением цепи и измеряют его в Омах. Графически электрические процессы в емкости представлены на рис. 2.13, 2.14.
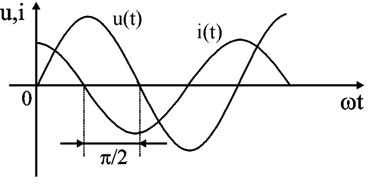
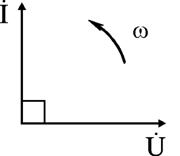Рис.
2.13 и 2.14
9. Индуктивность в цепи переменного тока.
Зададим изменение тока в индуктивности по синусоидальному закону
i(t) = ImL sin(ωt + ψi).
Используем уравнение связи между током и напряжением в индуктивности
uL = L · di / dt
и получим
uL(t) = ωL · ImL cos(ωt + ψi).
Заменим cos на sin и получим
(2.18) uL(t) = ωL · ImL sin(ωt + ψi + 90°).
Формальная запись синусоидального напряжения имеет вид
(2.19) uL(t) = UmL sin(ωt + ψu).
Соотношения (2.18) и (2.19) будут равны если выполняется условие равенства амплитуд и фаз
(2.20) UmL = ωL · ImL, (2.21) ψu = ψi + 90°.
Уравнение (2.20) можно переписать для действующих значений
(2.22) UL = ωL · IL.
Уравнение (2.21) показывает, что фаза тока в индуктивности отстает от фазы напряжения на 90°. Величину XL = ωL в уравнении (2.20) называют индуктивным сопротивлением. Единицей его измерения является Ом. Графически электрические процессы в индуктивности представлены на рис. 2.10, 2.11.
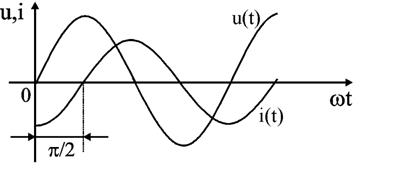
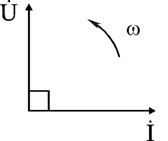
Рис. 2.10 и 2.11
10.Закон Ома для переменных токов.
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.
Если
ток является синусоидальным с циклической
частотой 
,
а цепь содержит не только активные, но
и реактивные компоненты
(ёмкости, индуктивности),
то закон Ома обобщается; величины,
входящие в него, становятся комплексными:
где:
U = U0eiωt — напряжение или разность потенциалов,
I — сила тока,
Z = Re−iδ — комплексное сопротивление (импеданс),
R = (Ra2 + Rr2)1/2 — полное сопротивление,
Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
Rа — активное (омическое) сопротивление, не зависящее от частоты,
δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.
При
этом переход от комплексных переменных
в значениях тока и напряжения к
действительным (измеряемым) значениям
может быть произведён взятием
действительной или мнимой части (но во
всех элементах цепи одной и той же!)
комплексных значений этих величин.
Соответственно, обратный переход
строится для, к примеру, 
подбором
такой 
что 
Тогда
все значения токов и напряжений в схеме
надо считать как 
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.