12.1.6. Фрагменты теории правки валов с помощью чеканки

Рассмотрим стержень, в верхнюю плоскость которого внедрен сферический индентор (рис. 12.9). При внедрении сферического индентора в упруго-пластическое тело вокруг индентора формируется зона интенсивной пластической деформации. При этом металл вытесняется из-под индентора и происходит его «выпучивание» над исходной плоскостью, образуется наплыв.

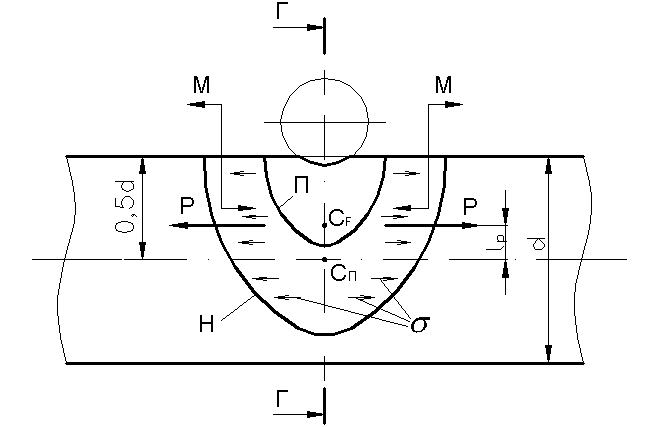
Рис. 12.9. Схема формирования изгибающего момента в зоне внедрения

сферического индентора.

Как было показано выше, пластическая деформация сопровождается уменьшением плотности и увеличением объема пластически деформированного металла. В связи с изложенным металл в зоне П стремится увеличить свои линейные размеры и изгибает стержень выпуклостью вверх. При этом нижележащие слои металла, которые не подверглись пластическому деформированию, испытывают упругую деформацию изгиба и поэтому стремятся вернуть стержень к исходной геометрической форме.

В результате в зоне П и в непосредственной близости от нее (в зоне Н) формируются остаточные напряжения сжатия. При этом чем глубже внедрен индентор в верхнюю плоскость стержня, тем больше зона П интенсивной пластической деформации, больше величина упругого изгиба стержня, больше зона распространения Н и величина остаточных напряжений сжатия.

Остаточные напряжения сжатия σ, суммируясь в зоне Н, в совокупности создают силы Р, приложенные в центре тяжести С_F зоны Н.

Если центр тяжести зоны Н лежит выше центра тяжести поперечного сечения стержня С_n, то возникает так называемое внецентренное растяжение стержня. При этом стержень испытывает продольное растяжение силами Р и чистый изгиб моментом М, который и изгибает стержень выпуклостью вверх (рис. 12.9).

Таким образом, механизм правки ППД сводится к следующему. Объем пластически деформированного в зоне П металла увеличивается, поэтому стержень упруго изгибается выпуклостью вверх. Его упруго деформированные слои стремятся вернуть стержень в исходное положение, поэтому в зоне П и Н формируются остаточные напряжения сжатия. Последние в сумме создают силы Р, приложенные в центре тяжести зоны Н. При этом стержень испытывает растяжение силами Р и чистый изгиб моментом М.

Следовательно, упругий изгиб стержня является следствием пластической деформации в зоне П, а остаточные напряжения сжатия в зоне Н, в свою очередь, являются следствием упругого изгиба стержня. Можно считать, что остаточные напряжения сжатия в зоне Н удерживают стержень в изогнутом состоянии. Поэтому, с другой стороны, их можно рассматривать как внешнюю нагрузку, вызывающую упругий изгиб стержня.

Такой подход дает возможность рассчитать изгибающий момент М, возникающий в зоне Н, и величину вызываемого им прогиба (величину правки) стержня.

Величину изгибающего момента М, возникающего при нанесении одного пластического отпечатка на верхнюю плоскость стержня, можно рассчитать по формуле:

, (12.2)

где l_P – плечо действия силы Р (расстояние от центра тяжести зоны Н до

центра тяжести поперечного сечения стержня);

Р – сила, созданная совокупным действием остаточных

напряжений сжатия в зоне Н; она равна:

, (12.3)

где  – средняя величина остаточных напряжений сжатия в зоне Н;

F – площадь зоны Н в вертикальном сечении, проходящем через центр

сферы индентора перпендикулярно плоскости эскиза (рис. 12.9).

Таким образом, для расчета изгибающего момента М необходимо прежде всего рассчитать площадь F фигуры, внутри которой сформированы остаточные напряжения сжатия, и координату ее центра тяжести y_F

(рис. 12.10).

Фигура с остаточными напряжениями сжатия состоит из совокупности четырех простых фигур (рис. 12.10):

, (12.4)

где F₁ – площадь фигуры ЕМАВС;

F₂ – площадь полукруга диаметром D;

F₃ – площадь криволинейной трапеции;

F₄ – площадь наплыва.

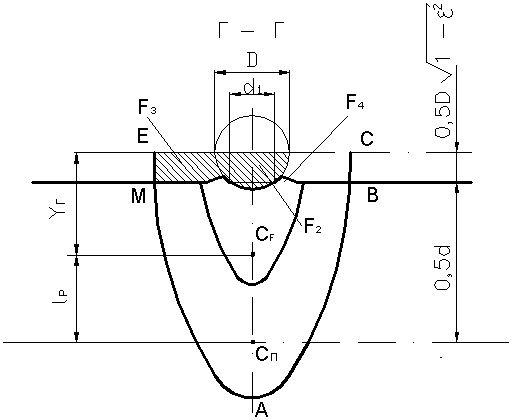
Рис. 12.10. Зоны, сформированные при внедрении сферического

индентора (сечение Г-Г по рис. 12.9)

Так как экспериментально установлено, что кривую EMABC можно интерпретировать как, параболу, площадь F₁ можно рассчитывать по формуле:

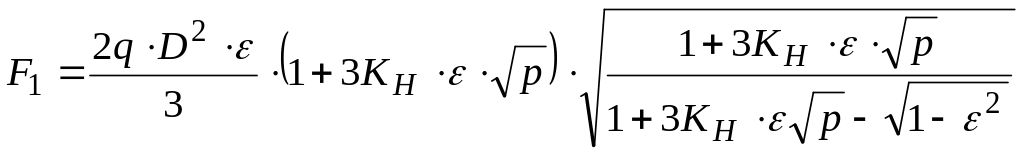, (12.5)

где ;

D – диаметр индентора, мм;

К_н – коэффициент, характеризующий глубину залегания остаточных

напряжений сжатия, К_н = (1,3–2);

q – коэффициент, характеризующий зону распространения пластической деформации в исходной плоскости детали, q = 1,8–2,2;

 – степень пластической деформации, , где

d₁ – диаметр отпечатка, мм.

Для расчета координаты центра тяжести y₁ кривой ЕМАВС получена формула:

(12.6)

Координата центра тяжести полукруга y₂ подсчитывается по формуле:

(12.7)

Площадь криволинейной трапеции F₃ равна:

. (12.8)

В результате вычисления двойного интеграла формула принимает вид:

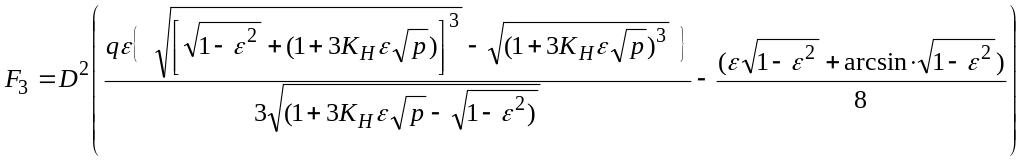(12.9)

Координата центра тяжести криволинейной трапеции равна:

(12.10)

Экспериментально установлено, что при значительных пластической деформации (ε=0,9–1) геометрическая форма наплыва соответствует треугольнику c основанием, лежащим в исходной плоскости детали.

Координата центра тяжести наплыва в формуле треугольника равна:

, (12.11)

где - высота треугольника, мм.

Таким образом, получены формулы для расчета всех слагаемых формулы (12.4). Координата центра тяжести y_F фигуры с остаточными напряжениями сжатия рассчитывается по формуле:

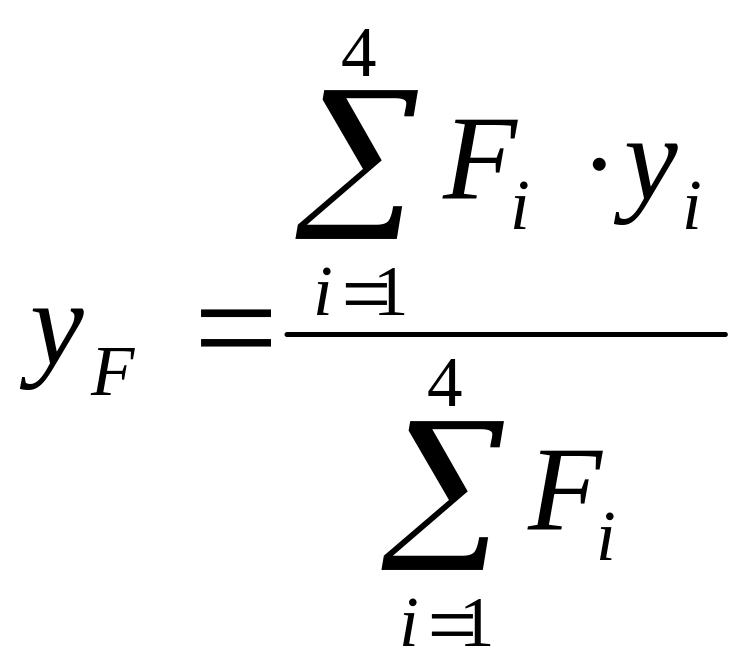
(12.12)

Плечо l_P действия силы P рассчитывается из размерной цепи (рис. 12.10):

. (12.13)

Формулы для расчета величины прогиба f (величины правки) валов при правке чеканкой для различных случаев взаимного расположения опор вала, мест нанесения пластических отпечатков и сечений, где производится измерение величины правки, имеют вид:

, (12.14)

где l₅ – длина, на которой происходит изгиб вала, мм;

I – осевой момент инерции поперечного сечения вала, мм⁴;

i – передаточное отношение, которое показывает, в каком отношении

прогиб вала в обработанном чеканкой сечении передается в то

сечение, где осуществляется измерение величины правки вала, мм.

Зависимость между величиной правки коленчатого вала по рис. 11.9

и режимом чеканки локального участка щеки выражается формулой:

, (12.15)

где Э_У – энергия удара бойка, Дж;

D₁ – диаметр сферической головки бойка, мм;

K₆ – коэффициент, определяемый экспериментально.