МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Одесский национальный морской университет
КАФЕДРА "ТЕХНИЧЕСКАЯ КИБЕРНЕТИКА"
“Исследование динамических систем с сосредоточенными параметрами”
курсовой проект по дисциплине
“Моделирование систем”
Вариант №3
Выполнила:
КСФ 3к. 4гр.
Красножон А.А.
Проверил:
Челабчи В.Н.
Одесса 2013
СОДЕРЖАНИЕ
C.
1 ИДЕНТИФИКАЦИЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 3
1.1 Исходные данные для идентификации 3
1.2 Методика идентификации 5
2. МОДЕЛИРОВАНИЕ РАБОТЫ ДИНАМИЧЕСКОЙ СИСТЕМЫ 11
2.1 Постановка задачи. 11
2.2 Приведение математической модели объекта к системе обыкновенных дифференциальных уравнений 1го порядка. 11
2.4 Решение системы уравнений (2.10) – (2.12) в среде Excel. 12
ИСПОЛЬЗОВАННЫЕ ЛИТЕРАТУРНЫЕ ИСТОЧНИКИ 19
ПРИЛОЖЕНИЕ 20
20
1Идентификация обыкновенного дифференциального уравнения первого порядка
1.1 Исходные данные для идентификации
Таблица 1.1 – Исходные данные
i |
|
X |
Y |
|
36 |
0,7 |
0,17642 |
0,46776 |
|
71 |
1,4 |
0,70412 |
0,65171 |
1 |
0 |
0,5111 |
-0,0021 |
|
37 |
0,72 |
0,16241 |
0,46711 |
|
72 |
1,42 |
0,68429 |
0,6578 |
2 |
0,02 |
0,57037 |
0,02018 |
|
38 |
0,74 |
0,20003 |
0,46303 |
|
73 |
1,44 |
0,68036 |
0,62665 |
3 |
0,04 |
0,63778 |
0,02664 |
|
39 |
0,76 |
0,19263 |
0,48233 |
|
74 |
1,46 |
0,6173 |
0,65478 |
4 |
0,06 |
0,64743 |
0,05224 |
|
40 |
0,78 |
0,17847 |
0,46413 |
|
75 |
1,48 |
0,60885 |
0,68115 |
5 |
0,08 |
0,73105 |
0,05404 |
|
41 |
0,8 |
0,18089 |
0,47608 |
|
76 |
1,5 |
0,60669 |
0,67088 |
6 |
0,1 |
0,75384 |
0,08541 |
|
42 |
0,82 |
0,20429 |
0,44497 |
|
77 |
1,52 |
0,59011 |
0,64932 |
7 |
0,12 |
0,80746 |
0,09307 |
|
43 |
0,84 |
0,19178 |
0,46403 |
|
78 |
1,54 |
0,52388 |
0,66376 |
8 |
0,14 |
0,85348 |
0,14104 |
|
44 |
0,86 |
0,22553 |
0,4331 |
|
79 |
1,56 |
0,50231 |
0,67155 |
9 |
0,16 |
0,88577 |
0,15399 |
|
45 |
0,88 |
0,25343 |
0,44007 |
|
80 |
1,58 |
0,50291 |
0,653 |
10 |
0,18 |
0,89535 |
0,17274 |
|
46 |
0,9 |
0,26062 |
0,46606 |
|
81 |
1,6 |
0,44376 |
0,65703 |
11 |
0,2 |
0,91707 |
0,19993 |
|
47 |
0,92 |
0,28527 |
0,41902 |
|
82 |
1,62 |
0,4426 |
0,64971 |
12 |
0,22 |
0,92652 |
0,24062 |
|
48 |
0,94 |
0,32958 |
0,43792 |
|
83 |
1,64 |
0,4398 |
0,67201 |
13 |
0,24 |
0,95225 |
0,27274 |
|
49 |
0,96 |
0,37583 |
0,43419 |
|
84 |
1,66 |
0,40294 |
0,69193 |
14 |
0,26 |
0,9359 |
0,28444 |
|
50 |
0,98 |
0,388 |
0,42075 |
|
85 |
1,68 |
0,38383 |
0,68716 |
15 |
0,28 |
0,95076 |
0,28148 |
|
51 |
1 |
0,39482 |
0,43841 |
|
86 |
1,7 |
0,37316 |
0,68759 |
16 |
0,3 |
0,89185 |
0,3028 |
|
52 |
1,02 |
0,46763 |
0,45388 |
|
87 |
1,72 |
0,32262 |
0,68719 |
17 |
0,32 |
0,88541 |
0,33071 |
|
53 |
1,04 |
0,47784 |
0,43324 |
|
88 |
1,74 |
0,34946 |
0,67352 |
18 |
0,34 |
0,89521 |
0,37944 |
|
54 |
1,06 |
0,53963 |
0,47746 |
|
89 |
1,76 |
0,33747 |
0,65844 |
19 |
0,36 |
0,84261 |
0,37471 |
|
55 |
1,08 |
0,53467 |
0,45941 |
|
90 |
1,78 |
0,33816 |
0,63734 |
20 |
0,38 |
0,79481 |
0,38238 |
|
56 |
1,1 |
0,57605 |
0,48671 |
|
91 |
1,8 |
0,31472 |
0,63315 |
21 |
0,4 |
0,75039 |
0,41624 |
|
57 |
1,12 |
0,59195 |
0,51045 |
|
92 |
1,82 |
0,29486 |
0,63979 |
22 |
0,42 |
0,71428 |
0,42523 |
|
58 |
1,14 |
0,64695 |
0,49085 |
|
93 |
1,84 |
0,32531 |
0,66895 |
23 |
0,44 |
0,6651 |
0,42745 |
|
59 |
1,16 |
0,65916 |
0,529 |
|
94 |
1,86 |
0,29967 |
0,63673 |
24 |
0,46 |
0,64913 |
0,46891 |
|
60 |
1,18 |
0,68849 |
0,5059 |
|
95 |
1,88 |
0,32022 |
0,62634 |
25 |
0,48 |
0,61464 |
0,47844 |
|
61 |
1,2 |
0,70905 |
0,54294 |
|
96 |
1,9 |
0,31904 |
0,63408 |
26 |
0,5 |
0,53054 |
0,48633 |
|
62 |
1,22 |
0,74357 |
0,55342 |
|
97 |
1,92 |
0,33404 |
0,62934 |
27 |
0,52 |
0,52437 |
0,48621 |
|
63 |
1,24 |
0,71962 |
0,56829 |
|
98 |
1,94 |
0,37066 |
0,65357 |
28 |
0,54 |
0,46631 |
0,4545 |
|
64 |
1,26 |
0,76585 |
0,57448 |
|
99 |
1,96 |
0,36862 |
0,63012 |
29 |
0,56 |
0,44443 |
0,46685 |
|
65 |
1,28 |
0,752 |
0,54671 |
|
100 |
1,98 |
0,4135 |
0,61543 |
30 |
0,58 |
0,35864 |
0,49994 |
|
66 |
1,3 |
0,76341 |
0,59653 |
|
|
|||
31 |
0,6 |
0,35054 |
0,46756 |
|
67 |
1,32 |
0,73519 |
0,56839 |
|
|
|||
32 |
0,62 |
0,28914 |
0,50413 |
|
68 |
1,34 |
0,71512 |
0,62105 |
|
|
|||
33 |
0,64 |
0,26889 |
0,5004 |
|
69 |
1,36 |
0,70604 |
0,60294 |
|
|
|||
34 |
0,66 |
0,22864 |
0,45891 |
|
70 |
1,38 |
0,73042 |
0,62774 |
|
|
|||
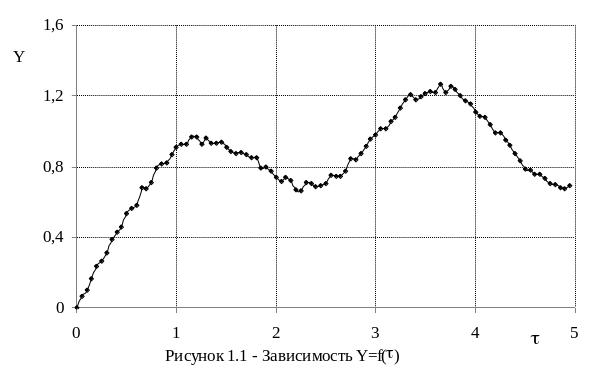
где - значение безразмерное время ;
X - значения воздействия (в безразмерном виде);
Y - значения реакции объекта (в безразмерном виде).
Данные таблицы отражены на рис. 1.1.
