
- •2. Критерий Макси Макса. Максиминный критерий Вальда.
- •3. Критерий оптимизма и пессимизма Гурвица.
- •5. Критерий Севиджа.
- •8. Нижняя и верхняя цена игры. Максиминные и минимаксные стратегии.
- •9. Решение матричных игр с седловой точкой.
- •10. Решение игры в смешанных стратегиях для платежной матрицы 2х2.
- •11. Принцип доминирования. Доминирующие и дублирующие стратегии.
- •12. Геометрическое решение игры в смешанных стратегиях(2х n)
- •13. Геометрическое решение игры в смешанных стратегиях (nх2).
- •17. Симплексный метод решения задачи линейного программирования.
- •18. Алгоритм составления симплексной таблицы. Преобразование симплексной таблицы.
- •19. Двойственные задачи линейного программирования.
- •20. Биматричные игры. Основные понятия.
- •23. Решение биматричной игры .
- •Раздел II .
- •24. Кооперативные игры.
- •25. Определение характеристической функции. Её свойства.
- •26. Дележи в кооперативных играх.
- •30. Решение игры по Нейману Моргенштерну.
- •31. Вектор Шепли.
- •32. Позиционные игры.
- •34. Информационные множества. Нормализация игры.
- •35. Позиционные игры с полной информацией.
- •37. Дифференциальные игры. Определение дифференциальной игры преследования.
23. Решение биматричной игры .
Биматричная игра 2х2
А11 |
А12 |
А21 |
А22 |
А=
B11 |
B12 |
B21 |
B22 |
В =
Р – частота применения 1 игроком стратегии (А1)
1-Р – частота применения стратегии (А2)
q – частота применения стратеги (В1)
q – частота применения стратегии (В2)
Формулы
На (р, q) ; Нв (р, q)
1. На (р, q) = а11*(р q) + р(1- q) + а21*(1-р)q + а22*(1-р)(1- q)
На = (а11-а12-а21+а22)р q + (а12-а22)р + (а21-а22)* q + а22
Нв = (в11-в12-в21+в22)р q + (в12-в22)р + (в21-в22)* q + в22
Введем следующие обозначения:
С = А11- А12- А21+А22
D = B11- B12- B21+B22
α = A22-A12
β = B22-B21
Ɣ = А21-А22
Δ = B12-B22
Ha(p;q) = C*(pq) – αp+ Vq +A22
(*)
Hb(p;q) = D*(pq) – Δ p + βq + B22
Раздел II .
Определение: Пара чисел р* и q*, 0≤ р*≤ 1; 0 ≤ q*≤1.
Определим равновесие, если выполнены 2 условия;
1. (Неравенство)
1.1 На (рq) < Ha(p*,q*) Ɣ p ϵ [0;1]
1.2 HB(p*q) ≤ HB(p*q*)
где, На (средний выигрыш 1 го игрока)
НВ (средний выигрыш 2 го игрока)
Неравенство (1) означает стратегии (p*q*) – определяем равновесие, если отклонение одного из игроков или условие, что другой игрок сохраняет свой выбор приводит к тому, что выигрыш относившегося игрока только уменьшается, таким образом, отклонение от равновесия не выгодно самому игроку.
24. Кооперативные игры.
Введение. Игра называется кооперативные , если в ней игрокам разрешено обсуждать свои стратегии и договор о совместных действиях игры образуют коалицию.
Теория кооперативных игр изучает тип коалиции который образуется в процессе игры.
Обозначим через N множество всех 4 игроков, игроков нумерации.
N=1,2,3…n. Коалиция показывает любое множество SCN S- по S множеств N.
число коалиций составлений из R игроков= Ckn
n=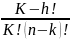 =
=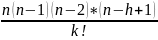
Число всевозможной коалиций:
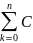 kn=2n
kn=2n
создание коалицию S множество игроков коалиции действует как один игрок против остальных игроков. Выигрыш коалиций S сумма выигрыша всех игроков этой коалиции.
Опр. Характеристическая функция называется адетивной, если
V(A
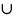 B)=
V(A)+V(B) (2)
B)=
V(A)+V(B) (2)
 A1B
A1B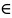 N
N
A
B=
Если равенство (2) выполняется для любых A B= , двух не пересекающих множеств.
Теорема:
Характеристическая функция является аддитивной когда и только тогда, когда выполняется равенство.
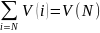 (3),
где
(3),
где
V(i)- выигрыш игрока с номером i
V(N)-выигрыш коалиции, соответствующей из все N игроков.
Доказательство: чтобы получить формулу (3)нужно показ умножить на имеющей на пересечение и принять формулу (2).
Возьмем две не переменные множители
S и L не пересекаются
S L= , тогда
V
(S)+V(L)
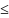 V(S
L)
V(S
L)
 V(S)
(1`)
V(S)
(1`)
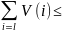 V(L)(2`)
V(L)(2`)
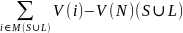 (3`)
(3`)
Отсутствие А \В – разность 2 множителей, которые состоят их элементов принадлежит множеству А и не принадлежит множителю В.
V(S L)+V (N \S L) V(N)
V(N)=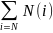
Если сложить неравенство (1`)+(2`)+(3`), то в левой части получится
V(N
)=
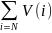 )
V(S)+
V(L)+V(N\S
L)
V(N)
(4`)
)
V(S)+
V(L)+V(N\S
L)
V(N)
(4`)
Все неравенства должны быть равенствами.
Теорема доказана.
Опр. если характер функции является аддитивной, т.е выполняется равенство.
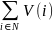 =V(N)
=V(N)
Тогда кооперативная игра называется не существенной.
Опр. Кооперативная игра называет существенная, если выполняется неравенство.
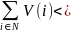 V(N)
V(N)
Игра существенная если выигрыш вне коалиции .
S дележи в кооперативных играх. Одна из основных задач кооперативной игры как поднять выигрыши. Если в результате распределения выигрыш коалиции.
Опр. Дележом называется вектор X= (x1, x2,… xn)
