
- •2. Критерий Макси Макса. Максиминный критерий Вальда.
- •3. Критерий оптимизма и пессимизма Гурвица.
- •5. Критерий Севиджа.
- •8. Нижняя и верхняя цена игры. Максиминные и минимаксные стратегии.
- •9. Решение матричных игр с седловой точкой.
- •10. Решение игры в смешанных стратегиях для платежной матрицы 2х2.
- •11. Принцип доминирования. Доминирующие и дублирующие стратегии.
- •12. Геометрическое решение игры в смешанных стратегиях(2х n)
- •13. Геометрическое решение игры в смешанных стратегиях (nх2).
- •17. Симплексный метод решения задачи линейного программирования.
- •18. Алгоритм составления симплексной таблицы. Преобразование симплексной таблицы.
- •19. Двойственные задачи линейного программирования.
- •20. Биматричные игры. Основные понятия.
- •23. Решение биматричной игры .
- •Раздел II .
- •24. Кооперативные игры.
- •25. Определение характеристической функции. Её свойства.
- •26. Дележи в кооперативных играх.
- •30. Решение игры по Нейману Моргенштерну.
- •31. Вектор Шепли.
- •32. Позиционные игры.
- •34. Информационные множества. Нормализация игры.
- •35. Позиционные игры с полной информацией.
- •37. Дифференциальные игры. Определение дифференциальной игры преследования.
18. Алгоритм составления симплексной таблицы. Преобразование симплексной таблицы.
Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств:
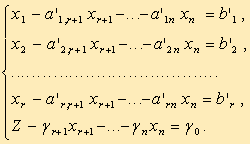
Далее эта система оформляется в виде симплекс-таблиц:
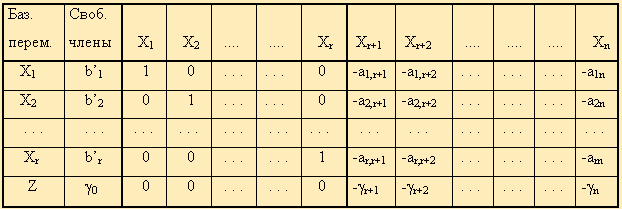
Примечание. Названия базисных переменных здесь взяты лишь для определенности записи и в реальной таблице могут оказаться другими.
Порядок работы с симплекс таблицей
Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению.
Алгоритм перехода к следующей таблице такой:
просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов
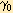 )
выбирается наименьшее отрицательное
число при отыскании max,
либо наибольшее положительное при
задачи на min.
Если такового нет, то исходное базисное
решение является оптимальным и данная
таблица является последней;
)
выбирается наименьшее отрицательное
число при отыскании max,
либо наибольшее положительное при
задачи на min.
Если такового нет, то исходное базисное
решение является оптимальным и данная
таблица является последней;просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;
среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называетсяразрешающим, а строка в которой он находится ключевой;
в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:
разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы.
строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место.
в новой таблице все элементы ключевого столбца = 0, кроме разрезающего, он всегда равен 1.
столбец, у которого в ключевой строке имеется 0,в новой таблице будет таким же.
строка, у которой в ключевом столбце имеется 0,в новой таблице будет такой же.
в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы:
19. Двойственные задачи линейного программирования.
Пусть дана задача линейного программирования
F(x) = c1x1 + … + cmxn → max
а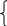 11х1
+
а12х2
+ … + сm1хn
≤ в1
11х1
+
а12х2
+ … + сm1хn
≤ в1
а21х1 + а22х2 + … + сm2хn ≤ в2
....аm1х1 + аm2х2 + … + сmnхn ≤ вm
Двойственной задачей является задача
Ζ (Y)= в1у1 + в2у2 + … + вmуm → min
а 11у1
+
а12у2
+ … + сm1уn
≥ с1
11у1
+
а12у2
+ … + сm1уn
≥ с1
а21у1 + а22у2 + … + сm2уn ≥ с2
….
аn1у1 + аn2у2 + … + сmnуn ≥ сm
yj ≥0, j = 1, 2 … m
y1, y2…ym – неизвестные двойственной задачи
Неизвестных в двойственной задачи столько, сколько ограниченных неравенств в двойственной задачи. Соответствующее число ограниченной двойственной задачи равно числу неизвестной двойственной задачи. Если матрицу обозначить через (А). Если одна из пары двойственной задачи имеет оптимальное решение, то двойственная задача так же имеет оптимальное решение, причём значение целевых функций на оптимальном решении совпадают.
Если одна из задач не имеет решения, то так же не имеет решения и двойственная задача. Это утверждение позволяет сводить задачи на min, max.
Пример: Ζ (x) = 6x1 + 7х2 + 9x3 → min
1 х1
+
2х2
+ 3х3
≥ 5
х1
+
2х2
+ 3х3
≥ 5
1х1 + 1х2 + 1х3 ≥2
1х1 + 2х2 + 6х3 ≥7
Х1≥0; Х2≥0; Х3≥0
F(Y)=
5у1
+ 2у2
+ 4у3
→ max
A
=
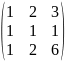 AT
=
AT
=
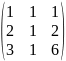
1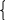 у1
+
2у2
+ 1у3
≤ 6
у1
+
2у2
+ 1у3
≤ 6
2у1 + 1у2 + … + 2у3 ≤ 7
3у1 + 1у2 + 6у3 ≤ 9
Формулы вычисления среднего выигрыша
Чтобы найти средние или математические ожидания нужно каждое значение случайной величины умножить на соответствующую вероятность и результат сложить. Значению aij соответствующей вероятности рi , qj
aij соответствующая вероятность рi , qj ; НА(Р,Q)
НА(Р,Q)
=
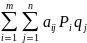 (для первого)
(для первого)
НB(Р,Q)
=
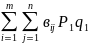 (для второго)
(для второго)
