1. Принятие решений в условиях неопределенности. (Егорова)

При решении социально-экономических задач приходиться принимать противоречивые интересы относящиеся к различным лицам и организациям. В таких случаях традиционные методы организационно конфликтный характер, не предполагая вражды между участниками, а свидетельствует и различных интересах, подобная ситуация вызвала математический характер под названием теория игр.

Теория игр - изучает процессы принятия оптимальных решений, это раздел математики.

Математическая теория игр была разработана американским учёным Джордоном Неймоном и Марген Штеймах в 1994 году, как средство математического подхода к явлениям конкурентной экономики. Игрой называют всякую конфликтную ситуацию изучаемую в теории игр, и представляющую упрощённую модель ситуации, от реальной ситуации игра отличается тем, что не включается второстепенным фактором, и ведётся по вполне определённым правилам. Всякая игра включает в себя 3 элемента: Игроков

Правила игры Оценку результатов действий игроков

Стратегией игрока называют совокупность правил определяющих выбор ситуации в сложившийся ситуации.

Оптимальной стратегией игрока называют такую, которая обепечит максимальный выигрыш.Вся теория игр заключается в том чтобы определить оптимальную стратегию для каждого игрока. Игры с природой Природа - это объективная действительность, и незаинтересованная сторона поведение которой неизвестно. Изучение игр с природой начинается с платёжной матрицы. фЛПР - лицо принимающее решение( у него много стратегий А_1, А_2, А₃…А_n)

У природы имеется n возможных состояний(П₁, П₂, П₃…П_n)

Платёжная матрица имеет вид:

	П1	П2		Пn
A1	d11	d12
A2	d21	d22		d2n
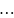
An	dm1	dm2		dmn

2. Критерий Макси Макса. Максиминный критерий Вальда.

С его помощью определяется страте­гия, максимизирующая максимальные выигрыши для каждого состояния природы. Это критерий крайнего оптимизма. Наилуч­шим признается решение, при котором достигается максималь­ный выигрыш, равный  .

Нетрудно увидеть, что для матрицы А наилучшим решением будет А₁, при котором достигается максимальный выигрыш - 9.

Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствовать­ся принципом «или пан, или пропал».

Максиминный критерий Вальда. С позиций данного крите­рия природа рассматривается как агрессивно настроенный и сознательно действующий противник типа тех, которые проти­водействуют в стратегических играх (см.гл. 2). Выбирается ре­шение, для которого достигается значение  .

Для платежной матрицы А (3.1) нетрудно рассчитать:

• для первой стратегии (i = 1)  ;

• для второй стратегии (i=2)  ;

• для третьей стратегии (i=3)  .

Тогда   , что соответствует второй стратегии A₂ игрока 1.

В соответствии с критерием Вальда из всех самых неудач­ных результатов выбирается лучший (W = 3). Это перестрахо­вочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определя­ется отношением игрока к риску.

3. Критерий оптимизма и пессимизма Гурвица.

Согласно критерию Гурвица оптим. стратегия выбирается по след формуле: 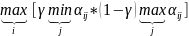Она содержит наимен. и наиб выигрыш γ-степень пессимизма. 0≤γ≤1. Заметим, что если γ=0, y=0, то этот критерий совпадает с критерием Макси Макса, если у=1, то с Вальда. Кр. гурвица применяется, когда о вероятностях появления разл ЛПР ничего не известно. В этом отличие Гурвица от Вальда.

4. Критерий Лапласа. Критерий Байеса.

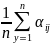основывается на предположение о том, что все состояния природы равновероятностны. Для каждой стратегии находим мат.ожидание.(сред. выигрыш 1, а затем стратегию максимиз средний выигрыш. - средний выигрыш.

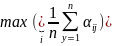
Критерий Байеса( критерий максимального мат. ожидания) При его использовании известны вероятности Р1,Р2, Рн, с которыми природа находится в состоянии соответствен П1, П2, Пн. Для каждой стратегии вычисляем величину 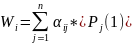- имеет смысл мат ожидания. Затем выбираем такую стратегию, для которой величина (1) 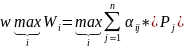критерий лапласа явл случ случаем Байеса, когда все вероятности равны.

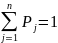
5. Критерий Севиджа.

Выбирая 1 из возможных решений останавливается на той стратегии, которая ведет к наименее тяжелым последствиям. За последствия отвечает риск. Элементы матрицы рисков отметим через эл-ты r_ij

   

Для матрицы R (3.2) нетрудно рассчитать:

• для первой стратегии (i=1)  ;

• для второй стратегии (i=2)  ;

• для третьей стратегии (i=3)  .

Минимально возможный из самых крупных рисков, равный 4, достигается при использовании первой стратегии А₁.

6. Критерий Ходжа-Лемана.

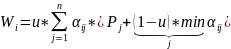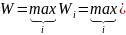Сначала вычисляется величина . Выбираем, когда эта стратегия наибольшая ]. У-параметр досьоверности о вероятностях состояния природы. Этот критерий явл промежуточным между критерием байеса и Вальда. Кр Ходжа-Лемана переходит в Байеса, когда у=1 и переходит в критерий вальда, когда у=0

7. Антагонистические игры. основные понятия.

Опр: Игра называется парной если в ней участвуют 2 игрока и множественной если игроков больше 2х.

Опр: Игра называется онтогонистической если выигрыш одного из игроков равен проигрышу другого.

Опр: Ходом игрока называется выбор одного из, предусмотренных правилами, действий.

Опр: Личный ход – сознательный выбор игроком 1го из возможных ходов.

Опр: Случайный ход – случайный выбор игроком своего хода.

В дальнейшем мы будем рассматривать только личные

Опр: Стратегия – совокупность правил, определяющих выбор действия игрока, при каждом личном ходе, в зависимости от сложившейся ситуации.

Опр: Игра называется конечной если у каждого игрока имеется конечное число стратегий.

Опр: Стратегия называется оптимальной если она позволяет 1му игроку получить максимальный выигрыш, когда второй придерживается своей стратегии. Соответственно 2й игрок должен иметь минимальный проигрыш, когда 1й придерживается своей стратегии.

Опр: Целью теории игр является определение оптимальных стратегий для каждого игрока.