33. Интегрирование некоторых трансцендентных функций (arcsin X, ln X, ex и др.)
34. Понятие определенного интеграла. Его свойства.
(3)
Если существует предел (3), не зависящий
от способа разбиения отрезка [a ;b]
и выбора точек
,
то этот предел будем называть определенным
интегралом функции f (х) на
отрезке [a ; b] и обозначать символом
,
т. е.
Функция f (х)
в этом случае называется интегрируемой
на отрезке [a ;b] .
При этом f
(х) называется подынтегральной
функцией,
-
подынтегральным выражением,
числа a и b - пределами
интегрирования
(a — нижний
предел, b — верхний
предел),
а сумма
-
интегральной суммой.
Теорема.
Если функция f (х) непрерывна
на отрезке [a ;b], то она интегрируема
на этом отрезке.
1) Путь s, пройденный
точкой по прямой за время
co
скоростью v = v (t) (v
(t)непрерывна на
),
есть
(механический
смысл определенного интеграла).
2) Если функция f (x) непрерывна
и неотрицательна на отрезке [a ; b],
то
представляет
собой площадь криволинейной трапеции,
ограниченной сверху графиком функции
y = f (х), снизу отрезком [a ; b]
осиОх и с боков отрезками прямых х
= а, x = b
(геометрический смысл
определенного интеграла).
Свойства:
По определению
полагают, что определенный интеграл от
функции с равными верхним и нижним
пределами интегрирования равен нулю:
.
1. Постоянный
множитель можно выносить за знак
определенного интеграла:
2. Определенный интеграл
от суммы двух функций равен
сумме определенных интегралов от этих
функций:
Это свойство распространяется на случай алгебраической суммы любого конечного числа функций.
3. При перестановке
пределов интегрирования
определенный интеграл меняет знак на
противоположный:
4.
Интеграл по отрезку равен сумме
интегралов по его частям:
35. Понятие несобственного интеграла первого и второго рода.
Определение:
Пусть функция
непрерывна
на полупрямой
.
Тогда несобственным интегралом первого
рода называется предел
.
Пример:
Признаки сходимости:
Если несобственный
интеграл равен конечному числу, говорят
что он сходится, если равен
или
не существует, то говорят что он не
сходится.
Пусть
и
непрерывны
на
и
.
Тогда:
1)Из сходимости большего интеграла следует сходимость, меньшего интеграла
2)Из расходимости меньшего интеграла следует расходимость большего интеграла.
Теорема:
Пусть функции
и
непрерывны
на
.
Если
,
то интегралы ведут себя одинаково.
Второго рода
Пусть
определена
на
,
терпит бесконечный разрыв в точке x=a и
.
Тогда:
Если
,
то используется обозначение
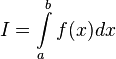и
интеграл называется несобственным
интегралом Римана второго рода. В
этом случае интеграл называется
сходящимся.Ес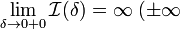ли
или
,
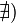то обозначение сохраняется, а
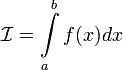называется
расходящимся к
,
или просто расходящимся.
Второго рода
Пусть
определена
на
,
терпит бесконечный разрыв при x=b и
.
Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Если функция
терпит
разрыв во внутренней точке
отрезка
,
то несобственный интеграл второго рода
определяется формулой:
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Пример
