20 Вопрос Первое правило Лопиталя

Рассмотрим функции  , которые бесконечно малЫ в некоторой точке  . Если существует предел их отношений  , то в целях устранения неопределённости   можно взять две производные – от числителя и от знаменателя. При этом:  , то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел   тоже должен существовать, в противном случае правило не применимо.

Что следует из вышесказанного?

Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)

Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного  !!!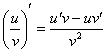

И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость  .

Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат: К неопределённости 0:0 применим первое правило Лопиталя: Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!

Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах:

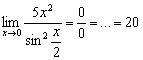
На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:

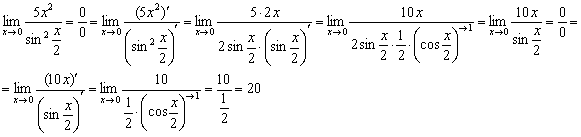
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).

Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные, следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам. Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.

Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности.

21. Принаки монотонности. Экстремум функции.

Функция y=f (x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство f(x1) < f(x 2) (f(x1) >f(x 2)).

Если дифференцируемая функция y = f (x) на отрезке [а, b] возрастает (убывает), то ее производная на этом отрезке f ¢ (x) > 0(f ¢ (x) < 0).

Точка x о называется точкой локального максимума ( минимума ) функции f(х), если существует окрестность точки x0 , для всех точек которой верно неравенство f (x) £ f(x0) (f (x)³ f (x0)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума . Если точка x о является точкой экстремума функции f (x), то либо f ¢ (x0) = 0, либо f ¢ (x0) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x0 - критическая точка. Если f ¢ (x) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x0 экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную

f ¢ (x) в окрестности точки x о и вторую производную в самой точке x0. Если f ¢ (x0) = 0, >0 (<0), то точка x о является точкой локального минимума (максимума) функции f (x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

22 Функция  f ( x ) называется  выпуклой  на интервале ( a, b ), если её график на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f (x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀  ( a, b ).

Функция  f ( x ) называется  вогнутой на интервале ( a, b ), если её график на этом интервале лежит  выше  касательной, проведенной к кривой  y = f (x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀  ( a, b ).

 

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x  ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x  ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

23

24.

25 делы ательные чкахпроміжку.

2

26

27

28

29