17 Вопрос Производные высших порядков
Если
функция 
дифференцируема
при всех 
,
то мы можем рассмотреть функцию 
,
сопоставляющую каждой точке 
значение
производной 
.
Эта функция 
называется
производной функции 
,
или первой
производной от
.
(Иногда саму исходную функцию
называют нулевой
производной и
обозначают тогда 
.)
Функция 
,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала 
,
которую мы обозначим 
и
назовём второй
производной функции
.
Если предположить, что вторая
производная 
существует
во всех точках
,
то она может также иметь производную 
,
называемую третьей
производной функции
,
и т. д. Вообще, 
-й
производной функции
называется
производная от предыдущей, 
-й
производной 
:
если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.
При 
первую,
вторую и третью производные принято
обозначать штрихами: 
или 
;
при прочих
--
числом в скобках в верхнем индексе: 
или 
.
Физический
смысл производной второго порядка
проясняется из того, что если первая
производная
задаёт
мгновенную скорость изменения значений
в
момент времени
,
то вторая производная, то есть производная
от
,
задаёт мгновенную скорость изменения
значений мгновенной скорости, то
есть ускорение значений
.
Следовательно, третья производная --
это скорость изменения ускорения (или,
что то же самое, ускорение изменения
скорости, поскольку, как очевидно следует
из определения, 
).
Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции, и мы обсудим его ниже.
Пример 4.19
Найдём вторую производную функции 
.
Первая производная равна
далее находим
18 Вопрос
В высшей математике очень часто используется понятие - дифференциал функции. В основном понятием дифференциал функции оперируют в неопределенных интегралах,дифференциальных уравнениях.
Для решения неопределенных интегралов используются различные способы сведения исходных неопределенный интегралов к уже существующим и известным. При этом будет использоваться понятие дифференциала функции, это понятие из дифференциального анализа. Напомним основное определение дифференциала функции.
Определение. Дифференциалом
функции 
(обозначается
через 
)
называется следующее выражение:
где dx -- дифференциал x при условии, что функция имеет производную.
Предположим, что существует следующее равенство функций:
тогда дифференциал от равенства есть
Приближённые вычисления с помощью дифференциала
Формулу
задающую определение дифференциала, можно записать в виде приближённого равенства
если
считать (при малых 
)
значение бесконечно малой величины 
много
меньшим, чем
.
Перенося 
в
правую часть, получаем:
где 
.
С учётом выражения дифференциала через
частные производные, находим, что
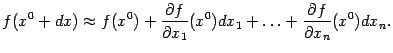
Эту
формулу можно применять для приближённого
вычисления значений функции
в
точках
,
если известны значения
и
её частных производных 
в
точке 
.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (24.1)
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (24.1) можно записать так:
dy=ƒ'(х)dх, (24.2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.