Билет 1.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

Случайным называют событие, которое при осуществлении условий S может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие «при бросании монеты выпал «герб»- случайное. Каждое случайное событие, в частности выпадение «герба», есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет,- она просто не силах это сделать.

Пространство элементарных событий

Элементарное событие – если в результате опыта может наступить одно и только одно из

событий ωi, то ωi называются элементарными событиями.

1. кость: ω1 - выпала 1

ω2 - выпала 2

ω6 - выпала 6

Пространство элементарных событий – это множество всех элементарных событий,

которые могут произойти в результате опыта.

А< Ω

Ω = {ωi}

Событие – это любое подмножество множества элементарных событий.

Замечание: достоверное событие совпадает с пространством элементарных событий.

Ø – невозможное событие.

Операции над событиями

1. Сумма событий

C = A+ B

суммой 2-х событий А и Вназывается такое событие С, которое происходит, если

происходит хотя бы одно из событий А и В.

при бросании игральной кости выпала А – 2 или 3 => А+В – 1,2 или 3; В – 1 или 2.

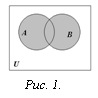
2. Произведение событий

C = A×B

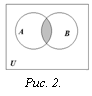
произведением событий А и Вназывается такое событие С, когда происходят одновременно два события А и В.

Пример:

Событие А – четкое количество очков

В – не более 3-х очков (3 ≤ )

A×B = 2

Замечание: если события А и В несовместны, то A×B = Ø - несовместное событие5

Пример:

А – 5 по математике

В – студент не умеет складывать обыкновенные дроби

A×B = Ø

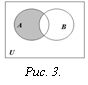
разность событий

C = A− B

событие С называется разностью событий, если оно происходит когда происходит событие А, но не происходит В.

Билет 2 классическое определение вероятности

ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Итак, вероятность события А определяется формулой:

где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.

Свойство 1. Вероятность достоверного события равна единице.

Свойство 2. Вероятность невозможного события равна нулю.

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Полная группа событий.

Теорема. Сумма вероятностей событий А1 , А2 , ..., Аn , образующих полную группу, равна единице:

Р (A1) + Р (А2) + ... + Р (Аn) = 1.

Теорема. Сумма вероятностей противоположных событий равна единице:

Доказательство базируется на том, что противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице

Билет 3

относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу практически произведенных испытаний. Таким образом, относительная частота А определяется формулой:

ример 2. Из 80 случайно выбранных сотрудников 3 человека имеют серьезные нарушения сердечной деятельности. Относительная частота появления людей с больным сердцем

В качестве статической вероятности принимают относительную частоту или число, близкое к ней.

ОПРЕДЕЛЕНИЕ (статистическим определением вероятности). Число, к которому стремится устойчивая относительная частота, называется статистической вероятностью этого события.

геометрическое определение вероятности: вероятность случайного события есть отношение площади области, благоприятствующей появлению события, к площади всей области.

где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.

Билет 4

1.5. Условная вероятность

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

В частности, отсюда получаем

.

Теорема сложения вероятностей. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В).

Вероятность суммы двух совместных событий выражается формулой:

Р(А+В) = Р(А) + Р(В) – Р(АВ).

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно m раз.

(формула полной вероятности). Пусть — полная группа событий. Тогда вероятность любого события может быть вычислена по формуле:

Билет 5.

Вероятность гипотез. Формулы Бейеса

Пусть событие A может наступить при условии появления одного из несовместных событий B₁,В₂,.. ., В_п, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события A определяется по формуле полной вероятности (см. § 2):

Р (А) = Р (В₁) (А)+ Р (В₂) (А)+ ...+ Р (В_n) (А). (*)

Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

Р_А(В₁), Р_А(В₂), ..., Р_А(В_п).

Найдем сначала условную вероятность Pa(B₁).По теореме умножения имеем

Р (АВ₁) = Р (А) Р_А (В₁) = Р (B₁) (A).

Отсюда

Р_А (В₁)= .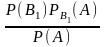

Заменив здесь Р (А) по формуле (*), получим

Р_А (В₁)= .

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы B_i (i=1, 2, ..., п) может быть вычислена по формуле

Р_А (В_i)= .

Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму — 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым—0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:

1)деталь проверил первый контролер (гипотеза B₁);

2)деталь проверил второй контролер (гипотеза В₂). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:

Р_А (В₁)= .

По условию задачи имеем:

Р(В₁)=0,6 (вероятность того, что деталь попадает к первому контролеру);

P(В₂) = 0,4 (вероятность того, что деталь попадет ко второму контролеру);

(A)= 0,94 (вероятность того, что годная деталь будет признана первым контролером стандартной);

(А) = 0,98 (вероятность того, что годная деталь будет признана вторым контролером стандартной).

Искомая вероятность

Р_А (В₁)= (0,6*0,94)/(0,6*0,94 + 0,4*0,98) 0,59.

Как видно, до испытания вероятность гипотезы В₁ равнялась 0,6, после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.

Билет 6.