Раздел 1.Специальная часть

1.1 Постановка задачи.

Разработать программу, моделирующую игру "Кости". Играющий называет любое число в диапазоне от 2 до 12 и ставку, которую он делает в этот ход. Программа с помощью датчика случайных чисел дважды выбирает числа от 1 до 6 ("бросает кубик", на гранях которого цифры от 1 до 6). Если сумма выпавших цифр меньше 7 и играющий задумал число меньшее 7, он выигрывает сделанную ставку. Если сумма выпавших цифр больше 7 и играющий задумал число большее 7, он также выигрывает сделанную ставку. Если играющий угадал сумму цифр, он получает в четыре раза больше очков, чем сделанная ставка. Ставка проиграна, если не имеет место ни одна из описанных ситуаций. В начальный момент у играющего 100 очков. В программе должно присутствовать графическое изображение поверхности кубика при каждом ходе игрока.

Данная программа позволяет немного отвлечься от повседневных дел, а также является хорошой разминкой после тяжелой работы. Мне нравится эта программа тем, что я её сделала сама а также тем, что у неё более низкая цена.

1.2 Модель задачи.

На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, т. е. возникают ситуации, в которых две стороны преследуют различные цели и результаты действия каждой из сторон зависят от мероприятий противника (или партнера). Ситуация, в которой эффективность принимаемого одной стороной решения зависит от действий другой стороны, называется конфликтной. Конфликт всегда связан с определенного рода разногласиями (это не обязательно антагонистическое противоречие). Конфликтная ситуация называется антагонистической, если увеличение выигрыша одной из сторон на некоторую величину приводит к уменьшению выигрыша другой стороны на такую же величину, и наоборот. В экономике конфликтные ситуации встречаются очень часто и имеют многообразный характер. Например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Каждый из них имеет свои интересы и стремится принимать оптимальные решения, помогающие достигнуть поставленных целей в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера и учитывать решения, которые эти партнеры будут принимать (они заранее могут быть неизвестны). Чтобы в конфликтных ситуациях принимать оптимальные решения, создана математическая теория конфликтных ситуаций, которая называется теорией игр. Возникновение этой теории относится к 1944 г., когда была издана монография Дж. фон Неймана «Теория игр и экономическое поведение» Игра – это математическая модель реальной конфликтной ситуации. Стороны, участвующие в конфликте, называются игроками. Исход конфликта называется выигрышем. Правила игры – это система условий, определяющая варианты действий игроков; объем информации каждого игрока о поведении партнеров; выигрыш, к которому приводит каждая совокупность действий. Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Мы будем рассматривать только парные игры. Игроки обозначаются A и B. Игра называется антагонистической (с нулевой суммой), если выигрыш одного из игроков равен проигрышу другого. Выбор и осуществление одного из вариантов действий, предусмотренных правилами, называется ходом игрока. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из вариантов действий (например, в шахматах). Случайный ход – это случайно выбранное действие (например, бросание игральной кости). Мы будем рассматривать только личные ходы. Стратегия игрока – это совокупность правил, определяющих поведение игрока при каждом личном ходе. Обычно в процессе игры на каждом этапе игрок выбирает ход в зависимости от конкретной ситуации. Возможно также, что все решения приняты игроком заранее (т. е. игрок выбрал определенную стратегию). Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной – в противном случае. Цель теории игр – разработать методы для определения оптимальной стратегии каждого игрока. Стратегия игрока называется оптимальной, если она обеспечивает этому игроку при многократном повторении игры максимально возможный средний выигрыш (или минимально возможный средний проигрыш независимо от поведения противника).

Пример 1. Каждый из игроков, A или B , может записать, независимо от другого, цифры 1, 2 и 3. Если разность между цифрами, записанными игроками, положительна, то A выигрывает количество очков, равное разности между цифрами. Если разность меньше 0, выигрывает B. Если разность равна 0 – ничья. У игрока A три стратегии (варианта действия): A₁= 1 (записать 1), A₂= 2, A₃= 3, у игрока  тоже три стратегии: B₁, B₂, B₃.

B     A	B1= 1	B2= 2	B3= 3
A1 = 1	0	-1	-2
A2= 2	1	0	-1
A3= 3	2	1	0

Задача игрока A – максимизировать свой выигрыш. Задача игрока B – минимизировать свой проигрыш, т. е. минимизировать выигрыш A. Это парная игра с нулевой суммой.

Для реализации игры необходимо разработать алгоритм работы программы. В данной работе алгоритм заключается в организации пользовательского интерфейса, позволяющего вводить ставку и число на которое ставится. Затем пользователь нажимает кнопку "Бросить". Здесь необходимо имитировать вращение кубиков с их последующей остановкой. После чего необходимо подсчитать количество очков.

Для вывода граней кубиков их сначала необходимо нарисовать в графическом редакторе. На рисунке 1 представлены нарисованные грани.

Рисунок 1 – грани кубиков.

Следует обратить внимание на то что объемность граней достигается двумя путями:

1) нарисованные изображения имеют сложную цветовую насыщенность, за счет чего создается впечатление объемности;

2) углы каждой грани закрашены цветом (черным), который в программе будет интерпретироваться как прозрачный.

Организация входных и выходных данных.

Входных данных у программы нет.

Выходными данными является совокупность отображаемой информации на экране персонального компьютера.

Для разработки приложения игры “Кости” используется среда визуального программирования “Delphi. Проект программы содержит три окна:

1. Form1 — главное окно программы.

2. FrmRules— окно, содержащее правила игры.

3. AboutBox— окно, содержащее информацию о программе.

О кно Form1.

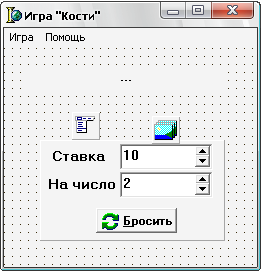
Для организации меню используется компонент tMainMenu. Текущий счет игры выводится в компонент tLabel. На панели (tPanel) находятся два поля ввода tSpinEdit, позволяющие вводить целые числа в нужном диапазоне. Кнопка "Бросить" (tBitBtn) запускает процесс игровой сессии.

Компонент tImageList представляет собой хранилище графических изображений одного размера. Кроме того, данный компонент инкапсулирует в себе набор методов по обработке графической информации. Например, в нем можно указать цвет, который будет считаться прозрачным при отображении. В программе кроме сервисных функций только одна процедура. Она вызывается по нажатию кнопки "Бросить"

В начале процедуры проверяется допустимость введенных значений ставки и числа на которое пользователь поставил. Если хотя бы одно из чисел имеет недопустимое значение, то пользователю выдается соответствующее сообщение и процедура заканчивает свою работу.

Далее происходит цикл вращения кубиков. В этом цикле случайным образом выбираются два числа в диапазоне от 0 до 5, соответствующих индексам картинок граней. Затем вызывается процедура перерисовки экрана, в которой на форму выводится соответствующие грани. После окончания цикла вращения происходит суммирование очков на обоих кубиках. После чего это число сравнивается со ставкой пользователя. В конце процедуры в зависимости от того выиграл он или нет изменяется суммарный счет и выводится сообщение о результатах текущего броска