3.Уравнение состояния идеального газа. Физический смысл газовой постоянной

Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

• Диаметр молекулы 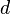пренебрежимо мал по сравнению со средним расстоянием между ними ( ).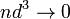

• Импульс передается только при соударениях, то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях.

• Суммарная энергия частиц газа постоянна, если отсутствует теплопередача и газ не совершает работы.

В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно полному импульсу, переданному при столкновении частиц со стенкой в единицу времени, внутренняя энергия — сумме энергий частиц газа.

По эквивалентной формулировке идеальный газ - такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака^[8], то есть:

где  — давление,  — абсолютная температура. Свойства идеального газа описываются уравнением Менделеева — Клапейрона ,

где - универсальная газовая постоянная,  — масса,  — молярная масса.

или

где  — концентрация частиц,  — постоянная Больцмана.

Для любого идеального газа справедливо соотношение Майера:

где — универсальная газовая постоянная, — молярная теплоемкость при постоянном давлении, — молярная теплоемкость при постоянном объёме.

Выводим формулу:

Используя зависимость давления идеального газа от его температуры и концентрации молекул

p = nkT ,

можно найти связь между основными макроскопическими параметрами газа — объемом V, его давлением p и температурой T.    Концентрация n молекул газа равна , (26.1)

где N — число молекул газа в сосуде объемом V. Число N можно выразить как произведение количества вещества на постоянную Авогадро N_A: . (26.2)

Из выражений (25.9), (26.1) и (26.2) получаем . (26.3)

Произведение постоянной Авогадро N_A на постоянную Больцмана k называется молярной газовой постояннойR. Молярная газовая постоянная равна

. (26.4)

Используя молярную газовую постоянную, выражение (26.3) преобразуем в уравнение . (26.5)

Количество вещества можно найти, зная массу вещества m и его молярную массу M: , (26.6)

поэтому уравнение (26.5) можно записать в такой форме: . (26.7)

Физический смысл: Газовая постоянная численно равна работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К

В системе СГС Газовая постоянная равна :

Удельная Газовая постоянная равна :  

33. Опред. циркуляционное давление в однотрубной системе водяного отопления.

Естест­венное циркуляционное давление, возникающее в систе­мах водяного отопления, в общем случае можно рас­сматривать как сумму двух величин: давления Δре.пр, возникающего за счет охлаждения воды в отопительных приборах, и давления Δре.тр вызываемого охлаждением воды в теплопроводах:

  ;                     (2.3)

ΔР_е = ΔР_{е, пр}+ ΔР_{е, тр},           (2.4)

 где DР_е– естественное циркуляционное давление в кольце; DР_{е, пр}  – давление, возникающее за счет остывания воды в приборах; DР_{е. тр}–то же за счет остывания воды в трубах, DР_{е. тр}учитывают только для систем с верхней разводкой и определяют по справочным данным [4, прил. 4]. В курсовом проекте DР_{е. тр}принимается 150 Па.

Давление, возникающее за счет остывания воды в приборах, определяется для систем с естественной и насосной циркуляцией по одним формулам

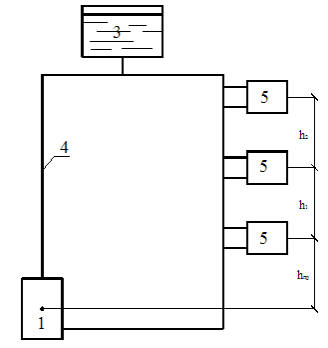
Рис. 2.8. Расчетная схема однотрубной системы водяного отопления с верхней разводкой и естественной циркуляцией. Обозначения см. на рис. 2.7

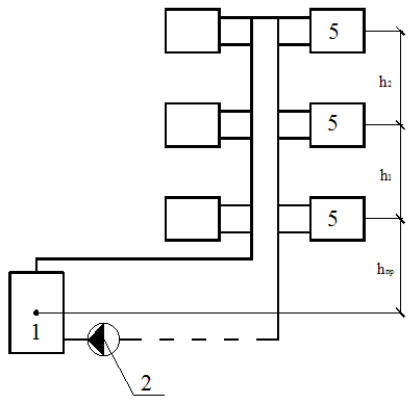
Рис. 2.9. Расчётная схема однотрубной системы водяного отопления с нижней разводкой и насосной  циркуляцией. Обозначения см. на рис. 2.7

ΔР_{е, пр}= gh (ρ₀ – ρ_г),       (2.5)

 где h – расстояние от центра котла или водонагревателя до центра нагревательного прибора в расчетном кольце, м (показано расстояние hдо центра прибора на первом этаже, через который проходит наиболее неблагоприятное циркуляционное кольцо); ρ₀ иρ_г– плотности горячей и охлажденной воды в системе отопления, кг/м³.

Для однотрубныхсистем водяного отопления при верхней разводке (рис. 2.8)

 ΔР_{е, пр}= gh_пр(ρ₀ – ρ_г) + gh₁(ρ₁ – ρ_г) ++ gh₂(ρ₂ – ρ_г) + …,                     (2.6)

 где h_пр – вертикальное расстояние от центра генератора тепла до центра нагревательного прибора первого эта­жа, м; h₁, h₂и т. д. – вертикальное расстояние от центра нагревательных приборов одного этажа до центра приборов следующего этажа, м; r_г, r₁, r₂, .... r_о – плотности воды, поступающей в систему, смеси воды на соответствующем участке и охлажденной воды, кг/м³.

Для однотрубныхсистем водяного отопления при нижней развод­ке (рис. 2.9)и размещении нагревательных приборов на нисходящей и восхо­дящей частях стояка в формуле (2.6) для участков, соответствующих h₁, h₂  и т. д., вместо r_гподставляют плотности воды на соответствующих участ­ках восходящего стояка

ΔР_{е, пр}= gh_пр(ρ₀ – ρ_г) + gh₁(ρ₄ – ρ₁) + gh₂(ρ₃ –ρ₂) + … .             (2.7)

 Плотности воды опреде­ля­ются в зависимости от ее температуры по справочным данным [4, прил. 3] или по прил. 5. Температуру воды на участках стояка одно­трубной системы водяного отопления определяют по формуле

 t_i= t_г – ,                                       (2.8) 

где t_г – температура горячей воды, подаваемой в систему отопления, °С; SQ_i– суммарная тепловая нагрузка приборов на стояке, расположенных выше (ранее) рассматриваемого участка по течению воды, Вт; Dt_ст – перепад температур теплоносителя на стояке, равный разности (t_г – t_о), °С; Q_ст–тепловая нагрузка стояка, Вт.

19. Определение коэффициента теплопередачи с использованием критериальных уравнений. Чаще всего в инженерной практике используются критериальные уравнения процесса теплоотдачи. При выборе критериального уравнения для определения коэффициентов теплоотдачи необходимо принимать во внимание следующее.

1. Учитывается характер теплообмена: без изменения агрегатного состояния вещества или с изменением.

2. Определяется режим движения теплоносителя, за который при вынужденном движении отвечает критерий Рейнольдса.

3. Характеризуется геометрическое расположение теплообменных труб: вертикальное или горизонтальное.

4. Характеризуется вид поверхности теплообмена: плоская, трубчатая.

5. Характеризуется тип конструкции теплообменника: кожухотрубчатый, змеевиковый, “труба в трубе” и т.д.

В общем виде критериальная зависимость для определения коэффициентов теплоотдачи имеет вид:

Nu=f (Re,Pr,Gr,…)

где:

Nu=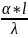 – критерий Нуссельта

Gr=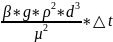 – критерий Грасгофа

Pr=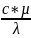 – критерий Прандтля

Re=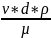 - критерий Рейнольдса

Здесь β – коэффициент объемного расширения, К-1

d – диаметр аппарата, м;

l – геометрический параметр аппарата, м;

c, λ, μ – удельная теплоемкость, коэффициент теплопроводности, динамическая вязкость (Дж/кг°К, Вт/м°К, Па·с, м2/с);

v – скорость потока, м/с;

ρ – плотность конденсата, кг/м3;

g – ускорение свободного падения;

Δt – разность температур стенки аппарата и среды, °К.

Таким образом, в общем виде выражения для расчета коэффициентов теплоотдачи можно записать в следующем виде:

α=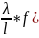 )