Билет 59. Поиск в двоичном дереве.
Функция выдает в результате работы ссылки на узел, содержащий необходимые данные или пустую ссылку, если нужная информация в дереве отсутствует.
function search (tree:Link;key:char):Link;
begin
if tree=nil then search:=nil
else
with tree^ do
if key<data then
search:=search(Left,key)
else
if key>data then
search:=search(Right,key)
else search:=tree;
end;
Т.к. поиск идет по одному единому пути от корня к нужной вершине то его можно программировать с помощью итерации.
function search (tree:Link;key:char):Link;
var endofsearch:Boolean;
begin
endofsearch:=false;
repeat
if tree:=nil then
endofsearch:=tree
with tree^ do
if key<data then tree:=Left
else
if key>data then tree:=Right
else
endofsearch:=true;
intil endofsearch
search:=tree;
end;
Если ключ не найден то результат nil.
function search (tree:Link;key:char):Link;
begin
with (tree<>nil) and (tree^.data<>key) do
if tree^.data<key then
tree:=tree^.Right
else
tree:=tree^.Left;
end;
Как и в случаи поиска в массиве сложность условия окончания наводит о мысли, о барьере.
function search (tree:Link;key:char):Link;
begin
S^.data:=key;
While tree^.data<key
then tree:=tree^.Right
else tree:=tree^.Left
search:=tree;
end;
Если в дереве с корнем 3 ключ со значением key не будет обнаружен т функция search получит значение S, а не nil как в первом случаи, т.е. будет указывать на барьер.
Типичный пример программы использ. динамичное размещение переменных с доступа к ним через ссылки. Задачей частотной словаря можно наз. поиск по дереву с включением.
Билет 60. Просмотр двоичного дерева.
Просмотр двоичного дерева может воспроизводиться рекурсивно: для каждого узла нужно выполнить три действия.
Исследовать узел
Просмотреть левое поддерево
Просмотреть правое поддерево
Эти три действия могут быть выполнены шестью разными последовательностями. Благодаря существованию традиционного соглашения о том, что левое поддерево всегда просматривается перед правым, число способов становится равным трём. Эти способы имеют следующие названия:
Прямой просмотр (исследуется сначала узел, потом левое, потом правое поддеревья (У,Л,П))
Обратный просмотр (Л,У,П)
Концевой просмотр (Л,П,У)
Рекурсивная процедура, выполняющая прямой просмотр двоичного дерева.
procedure preorder (tree: link);
begin if tree<>nil then
begin dosmth; {исследуем узел}
preorder (tree^.left);
preorder (tree^.right)
end;
end;
Другие виды просмотра могут быть получены путём перестановки трёх операторов, входящих в состав процедуры.
Обратный просмотр дерева приводит к возникновению упорядоченности узлов по алфавиту.
Билет 61. Удаление из дерева.
Не так просто как включение.
Простым оно будет в том случаи, когда удаляемый элемент является терминальным узлом или имеет одного потомка. Трудность заключается в удалении элемента с двумя потомками т.к. мы не можем указать одну ссылку на два направления. В этом случаи удаляемый элемент нужно заменить либо на самый правый элемент его левого поддерева, либо на самый левый элемент правого поддерева.
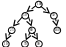Ясно
что такие элементы не могут иметь более
одного потомка.
Рекурсивная процедура delete различает три случая:
1. компонента с ключом х – нет;
2. компонента с ключом х – имеет всего одного потомка;
3. компонента с ключом х – имеет более 2 потомка.
procedure delete (x:integer;var p:Link);
var q:Link;
procedure del (var z:Link);
begin
if r^.right<>nil then
del (r^.Right) else
begin
q^.key:=r^.key;
q^.count:=r^.count;
q:=r; r:=f^.Left;
end;
end;
begin {delete}
if p=nil then
wreteln(‘word is not in tree’) else
if x<p^.key then delete (x,p^.Left) else
if x>p^.key then delete (x,p^.Right) else
begin
q:=p;
if q^.Right=nil then p:=q^.Left else
if q^.Left=nil then p:=q^.Right else
del(del^.Left);
end;
Вспомогательная рекурсивная процедура del вызывается только в третьем случае. Она спускается вдоль самой правой ветки левого поддерева удаляемого узла q^ и затем заменяет сущест. инфор. (ключ и счетчик) в q^ соответ. значениями самой правой компоненты r^ этого поддерева, после чего от r^ можно освободиться.
Двоичное дерево поиска представляет собой более удобную структуру для хранения данных, чем массив. При работе с таким деревом необходимо предварительно убедится что данные не поступают в порядке возрастания или убывания т.к. дерево в этом случаи выродится в линейный список. Во многих практических случаях, однако, данные поступают в существенно случайном порядке, что позволяет строить достаточно эффективное дерево, состоящее из n – узлов время необходимое для добавления/исключения узла пропорционально log2 n , тогда как линейный поиск пропорционален n.