Билет 57. Деревья. Двоичные деревья. Двоичные деревья поиска.
Предположим у нас некоторая структура, состоящая из записей связанных между собой системами ссылок. Причем каждая запись может содержать ссылки на несколько других записей. Так представляются направленные графы. Вершинами или узлами графа является записи, ссылки играют роль ребер. Частным случаем графа является дерево, которое имеет следующее св-во:
- подструктура связанных с некоторыми узлами не связаны между собой;
- существует узел наз. корнем, из которого просмотром конечного числа ребер может достичь любого узла дерева.
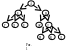
На рисунке узел А – это корень, узла Г,Д,Е,Ж,И,К,Л – терминал узла или листья.
Дерево является рекурсивной структурой. Рекурсивное определение: дерево либо пуста, либо состоит из узла содержащего ссылки на непересекающиеся деревья.
Каждый узел двоичного дерева имеет не более двух узлов отростков. Эти два отростка наз. левым и правым отросткам. Эти два отростка не являются взаимозаменяемыми.
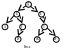
Для представления двоичного дерева в Паскале удобно пользоваться записями.
type Link=^Node;
Node=record
Data:char;
Left,Right:Link; End;
Просмотр двоичного дерева можно производится рекурсивно, для каждого узла нужно выполнить следующие действия:
1. исследовать узел, т.е. выполнить какие то операции;
2. просмотреть левое поддерево;
3. просмотреть правое.
Эти три шага могут выполнять шесть различных последовательности. Благодаря существующим традиционным соглашением о том, что левая поддерево всегда просматривается перед правым кол-во возможных способов снижается до трех. Три оставшихся способа имеют спец. наименования:
1. прямой просмотр – сначала исследуется узел затем левое и правое поддеревья;
2. обратный просмотр – исследуется левое поддерево узел правое;
3. концевой просмотр – узел исследуется после просмотра поддеревьев.
Рекурсивная процедура, выполняющая прямой просмотр дерева:
procedure preorder (tree:Link);
begin
if tree<>nil then
begin
dosomething(tree); {исследуем узел}
preorder(tree^.Left);
preorder(tree^.Right);
end;
end;
Другие виды просмотра могут быть получены путем перестановки трех операторов вход. во внутренний составной оператор. При различных порядках просмотра дерево изображенное на рис. а узлы исследуются в следующие последовательности.
След. последовательность: Д,Б,А,Г,В,Е,З,Ж,И
Обратная последовательность: А,Б,В,Г,Д,Е,Ж,З,И
Концевая: А,В,Г,Б,Ж,И,З,Е,Д
Обратная просмотр приводит к возникновению упорядочности узлов по алфавиту.
Дерево изображенное на рис. а является двоичным деревом поиска.
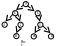
Дерево наз. двоичным деревом поиска, если для каждого узла ti все ключи в левом поддереве меньше ключа ti а ключи в правом поддереве больше ti.
В дереве поиска можно найти место каждого ключа, начиная от корня и переходя на левые и правые поддеревья в зависимости от значения ключа.
Билет 58. Добавление узла к двоичному дереву поиска.
к двоичному дереву один узел, сохраняя его упорядоченность.
procedure insert (var tree: Link; newdata: char);
begin
if tree=nil then
begin new(tree);
with tree^ do
begin Left:=nil; Right:=nil;
Data:=newdata;
end;
end;
end;
with tree^ do
if newdata<data then
insert(Left,newdata)
else
if newdata>data then
insert(Right,newdata);
else {продублировать информацию если равна}
end;