Билет 46. Сортировка шелла.
Некоторое усовершенствование сортировки простыми включениями было предложено Д. Л. Шеллом в 1959 году. Этот метод показан на следующем примере.
Сортировка с убывающими расстояниями:
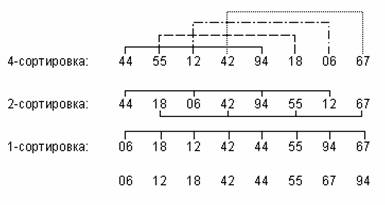
Расстоянием h между двумя элементами a[j] и a[i] называется положительная разность их индексов. Например, расстояние между элементами a[2] и a[6] равно 4 (h = 62).
На первом проходе отдельно группируются и сортируются (внутри группы) методом простого включения все элементы, отстоящие друг от друга на четыре позиции. Этот процесс называется 4-сортировкой. В нашем примере из восьми элементов каждая группа на первом проходе содержит ровно два элемента. После этого элементы вновь объединяются в группы с элементами, расстояние между которыми равно 2, и сортируются заново. Этот процесс называется 2-сортировкой. Наконец на третьем проходе все элементы сортируются обычной сортировкой включением (1-сортировка). Заметим, что группы, в которых последовательные элементы отстоят на одинаковые расстояния, никуда не передаются они остаются «на том же месте».
На каждом шаге в сортировке участвует либо сравнительно мало элементов, либо они уже довольно хорошо упорядочены и требуют относительно мало перестановок.
Очевидно, что этот метод дает упорядоченный массив, и что каждый проход будет использовать результаты предыдущего прохода, поскольку каждая i-сортировка объединяет две группы, рассортированные предыдущей (2i)-сортировкой. Также ясно, что приемлема любая последовательность приращений, лишь бы последнее было равно 1, так как в худшем случае вся работа будет выполняться на последнем проходе. Однако менее очевидно, что метод убывающего приращения дает даже лучшие результаты, когда приращения не являются степенями двойки.
Все t приращений обозначим через
h1, h2, ..., ht
с условиями
ht = 1, hi+1 < hi, i=1, …, t1.
Каждая h-сортировка программируется как сортировка простыми включениями.
Программа сортировки методом Шелла может иметь следующий вид:
Procedure ShellSort;
Const t=4;
Var i, j, k: index;
x: item; m: 1..t;
h: Array [1..t] Of integer;
Begin
H[1]:=9;
H[2]:=5;
H[3]:=3;
H[4]:=1;
For m:= 1 To t Do Begin
k:= h[m]; s:=-k; {место барьера}
For i:= k+1 To N Do Begin
X:=a[i];
j:= i - k;
if s=0 then s:=-k;
s:=s+1;
a[s]:=x;
While x < a[j] Do Begin
a[j+k]:=j;
j:= j - k;
End;
A[j+k]:=x;
End;
End;
End;
Билет 47. Сортировка с разделением(быстрая сортировка).
Метод сортировки разделением был предложен Чарльзом Хоаром (он любит называть себя Тони) в 1962 г. Этот метод является развитием метода простого обмена и настолько эффективен, что его стали называть "методом быстрой сортировки - Quicksort".
Основная идея алгоритма состоит в том, что случайным образом выбирается некоторый элемент массива x, после чего массив просматривается слева, пока не встретится элемент a[i] такой, что a[i] > x, а затем массив просматривается справа, пока не встретится элемент a[j] такой, что a[j] < x. Эти два элемента меняются местами, и процесс просмотра, сравнения и обмена продолжается, пока мы не дойдем до элемента x. В результате массив окажется разбитым на две части - левую, в которой значения ключей будут меньше x, и правую со значениями ключей, большими x. Далее процесс рекурсивно продолжается для левой и правой частей массива до тех пор, пока каждая часть не будет содержать в точности один элемент. Понятно, что как обычно, рекурсию можно заменить итерациями, если запоминать соответствующие индексы массива. Проследим этот процесс на примере нашего стандартного массива.
procedure qSort(var ar:array of real; low,high:integer);
var
x,w:item;
begin
i:=1;
j:=n;
{выбор случайного элемента}
repeat
while(a[i]<x) do i:=i+1;
while(a[j]>x) do j:=j-1;
if(i<=j) then begin
w:=a[i];
a[i]:=a[j];
until (i>j);
a[j]:=w;
i:=i+1;
j:=j+1;
end;
end;