В. Метод суперпозиции
Данный метод на важном физическом принципе: воздействие нескольких источников на какой-либо элемент линейной цепи можно рассматривать как результат воздействия на этот элемент каждого источника в отдельности независимо от других.
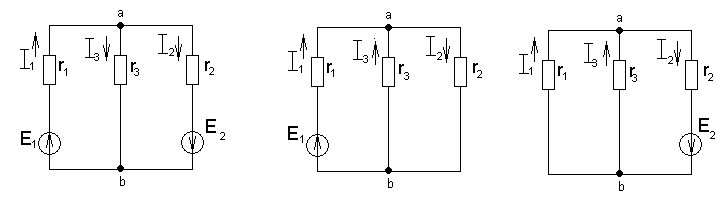
а) б) в)
Рис.1.27. Схема для расчета цепи методом суперпозиции
Условно исключаем из цепи все источники, кроме одного ( при этом сохраняем их внутренние сопротивления и цепи замкнутыми). Для рассматриваемой цепи исключаем
(рис.1.27.б).
Цепь рассчитываем методом, известным для простых разветвленных цепей, и определяем частные токи
.
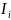Преобразованную в простую цепь
(рис.1.27.б) рассчитываем методом
свертывания:
Аналогично рассчитываем частные токи, создаваемые всеми другими источниками поочередно. Для рассматриваемой цепи токи создаваемые (рис.1.27.в.):
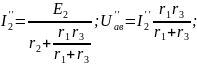
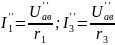
Определяем результирующие токи в ветвях, как алгебраическую сумму частных токов:
.
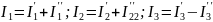Примечание: при расчете цепей методом суперпозиции целесообразно проверить решение по первому и второму законам Кирхгофа.
Данный метод наиболее нагляден, т.к. позволяет определить влияние каждого источника на распределение токов в ветвях. Однако он применим не во всех случаях, а лишь для линейных цепей, требует большого объема вычислений с достаточно высокой точностью.
Г. Метод узлового напряжения. Вывод расчетных соотношений.
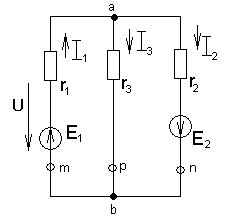
Рис.1.28. Схема для расчета цепи методом узлового напряжения.
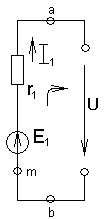
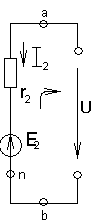
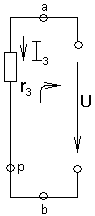
а) б) в)
Рис.1.29(а,б,в)
Допустим,
что в результате воздействия всех
источников между узлами а
и в установилось
результирующее напряжение
.
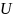Выберем и обозначим на схеме условные положительные направления токов в ветвях: в активных ветвях – по направлению ЭДС, в пассивных – по направлению .
Для
цепи (рис.1.29) составим для каждой
параллельной ветви (amв,
anв,
apв)
в отдельности
уравнения по второму закону Кирхгофа
и решим их относительно токов в ветвях
(
,
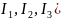заменив сопротивления ветвей их
проводимостями
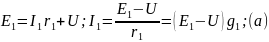
Уравнение по 1 закону Кирхгофа для узла а:
Подставим в него полученные выражения и решим относительно т.е.
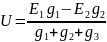
Для цепи с большим числом источников и ветвей
(1.8)
Результирующее напряжение между узлами в цепи, состоящей из набора параллельных ветвей, включенных между узлами, равно алгебраической сумме произведений ЭДС на проводимости активных ветвей, деленной на сумму проводимостей всех ветвей.
При составлении данного уравнения слагаемые в числителе записываются со знаком «+», если их направления совпадают.
Последовательность расчета цепей методом узлового напряжения.
Приводим цепь к набору параллельных ветвей, включенных между двумя узлами.
Выбираем условное положительное направление результирующего напряжения .
Вычисляем проводимости всех ветвей
.Определяем по формуле (1.8).
Примечание: если в результате расчета получается со знаком «-», это означает, что его действительное направление противоположно принятому.
Указываем на схеме действительное направление напряжения (если это необходимо).
Выбираем и обозначаем на схеме условные положительные направления токов в ветвях: в активных – по направлению ЭДС, в пассивных – по направлению .
Составляем уравнения по второму закону Кирхгофа для каждой ветви в отдельности (рис.129) и определяем токи в ветвях.
Примечание: Если какой-то ток получается со знаком « - », значит его направление противоположно принятому. По окончании расставив для одного из узлов уравнение по первому закону Кирхгофа.
Метод узлового напряжения позволяет достаточно просто рассчитать цепь. Однако он применим только для схем, проводимых к набору параллельных ветвей.