Расчет схемы рис.1.21

Заменим в схеме рис.1.21 треугольник резистором эквивалентной звездой , (рис.1.23).

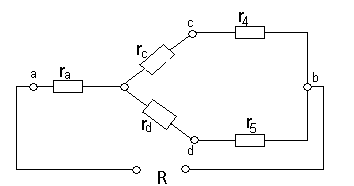
Рис.1.23. Эквивалентные преобразования схемы рис.1.21.

Далее схема свертывается изложенным методом.

1.1.13. Методы расчета электрических цепей постоянного тока а. Метод непосредственного применения законов Кирхгофа.

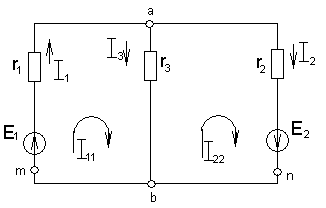
Рис.1.25.

1. Определяем количество ветвей в=3, узлов у=2, независимых контуров

2. Выбираем произвольно и обозначаем на схеме условные положительные направления токов в ветвях.

3. Составляем у-1=1 уравнений по первому закону Кирхгофа;

Для узла а:

4. Принимаем произвольно и обозначаем на схеме направления обхода независимых контуров.

5. Для этих контуров составляем уравнение по второму закону Кирхгофа

6. Совместно решаем уравнения (1.2) и (1.3) относительно токов в ветвях

7. Проставляем на схеме истинные направления токов в ветвях.

Метод универсален, нагляден и прост, но в случае трех – и более контурной цепи требует громоздких вычислений.

Б. Метод контурных токов.

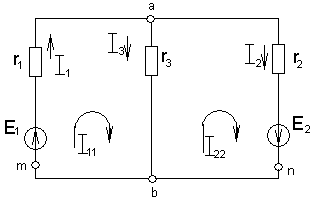
Рис.1.26.

1. Определяем количество ветвей в=3, узлов у=2 – и независимых контуров

2. Принимаем, что в каждом из выбранных течет свой автономный контурной ток. Выбираем произвольно и обозначаем на схеме их условные положительные направления (здесь по часовой стрелке). Обозначение

3. Для каждого контура составляем уравнения по второму закону Кирхгофа (направления обхода контуров соответствует контурным токам)

В этих уравнениях присутствуют и контурные токи, и токи смежных контуров, т.к. условно принято, что контурный ток течет только в пределах данного контура, следовательно, в смежной ветви текут два контурных тока

навстречу друг другу.

4. Вычисляем собственные сопротивления контуров, как сумму сопротивлений, входящих в данный контур, и обозначаем их

5. Вычисляем взаимные сопротивления смежные контуров, как сумму сопротивлений смежной ветви контуров , . При этом, если в смежной ветви контурные токи текут в противоположных направлениях, эти сопротивления записывают со знаком «-», а если в одном направлении, то со знаком «+».

6. Определяем контурные ЭДС, как алгебраическую сумму ЭДС, входящих в контур. Если направления ЭДС совпадает с контурным током, ей присваивается знак «+», если оно противоположно контурному току – знак « - ». Контурные ЭДС обозначаем

(1.7)

7. Переписываем систему уравнений (1.4) в канонической форме и присваиваем значение коэффициентом и свободным членам в соответствии с (1.5), (1.6.), (1.7).

8. Решаем последнюю систему уравнений относительно контурных токов . (Если в результате решения, какой-либо контурный ток получается со знаком «-», это означает, что его действительное направление противоположно ранее принятому).

9. Указываем на схеме рис. 1.26. истинные направления контурных токов

10. Определяем значение и направления токов в ветвях:

- если ветвь принадлежит только одному контуру, ток в ней по величине и направлению соответствует контурному;

- если ветвь смежная для двух контуров, ток в ней равен алгебраической сумме контурных токов смежных контуров, а направление определяется большим контурным током. Например, если

, то

11. Проставляем на схеме направления токов в ветвях (рис.1.26). При расчете цепи методом контурных токов решение целесообразно проверить по первому и второму законам Кирхгофа.

Этот метод позволяет сократить, число совместно решаемых уравнений ( для трехконтурной цепи с 6 до 3 ), однако он несколько формален и менее нагляден.