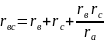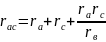- •Электротехника
- •Электрические цепи постоянного тока
- •Электрическая цепь и ее элементы
- •Признаки классификации электрических цепей
- •Задачи анализа и расчета электрических цепей
- •1.1.4. Э.Д.С., напряжение, ток и их условные положительные Направления
- •1.1.5. Сопротивление проводников
- •1.1.6. Источники эл. Энергии и схемы их замещения
- •1.1.7. Основные законы электрических цепей.
- •Лекция №2
- •1.1.8. Эл. Энергия и мощность в цепях постоянного тока
- •1.1.9 Простые эл. Цепи с последовательным соединением приемников
- •Расчет схемы рис.1.21
- •1.1.13. Методы расчета электрических цепей постоянного тока а. Метод непосредственного применения законов Кирхгофа.
- •Б. Метод контурных токов.
- •В. Метод суперпозиции
- •Г. Метод узлового напряжения. Вывод расчетных соотношений.
- •Метод эквивалентного генератора.
- •Последовательность расчета методом эквивалентного генератора.
- •Лекция №3
- •1.1.14. Баланс мощности в цепях постоянного тока.
- •1.1.15.Способы соединения источников электрической энергии.
- •1.1.16. Условие передачи максимальной мощности источника во внешнюю цепь.
- •Лекция №4
- •1.2.1 Основные понятия о синусоидальном переменном токе.
- •2. Процесс заряда конденсатора от источника постоянного напряжения
- •1.2.3. Действующее значение синусоидальных эдс, тока и напряжения.
- •4. Методы описания и представления синусоидального тока, эдс и напряжения
- •1.2.9 Цепь синусоидального тока с реальной катушкой индуктивности
- •1.3.1. Последовательный колебательный контур. Резонанас напряжений.
- •1.4. Трансформаторы.
- •1.4.1 Назначение и принцип действия трансформатора.
- •1.4.2. Холостой ход трансформатора.
- •1.4.3. Нагрузка трансформатора.
- •1.4.4. Схема замещения трансформатора с нагрузкой.
- •1.4.5. Короткое замыкание трансформатора.
- •1.4.6. Внешняя характеристика трансформатора.
- •1.4.7. Потери мощности и кпд трансформатора.
- •2. Основы электроники
- •2.1 Полупроводники. Зонная теория.
- •На рис. 1.1. Представлена схема энергетических зон
- •2. Собственные полупроводниковые приборы.
- •Примесные поупроводники
- •Различают:
- •2.1.2 Электронно - дырочный переход (р - n переход).
- •2.1.2.1 Процессы в p- n переходе при отсутствии внешнего источника.
- •2.1.2.2 Прямое включение p – n перехода.
- •2.1.3 Виды полупроводниковых диодов.
- •Iобр.(Iо) – среднее значение
- •Фотодиоды
- •2.1.4 Транзисторы
- •2.1.4.1 Униполярные (полевые) транзисторы
- •2.1.4.2 Полевые транзисторыс управляющим p-n переходом
- •2.1.4.2 Мдп транзистора
- •2.1.5.2 Устройство и принцип действия транзистора.
- •Ik зависит от iб и не зависит от Uкэ
- •2.1.5.4 Дифференциальные параметры бт
- •2.1.5.5 Предельные параметры бт
- •2.1.5.6 Схема замещения бт с оэ
- •Лекция № 12
- •2.2.1 Усилительный каскад на бт с оэ.
- •2.2.1.1 Динамический режим работы бт.
- •Для определения Ки требуется определить h – параметры
- •2.2.1.2 Усилители кпу
- •Блок схема включения усилителя
- •А. Входные данные усилителя
- •2.2.1.3 Однокаскадные усилители на бт с оэ
- •2.2.2. Обратные связи в усилителе
- •Влияние ос на основные технические показатели усилителя
- •1.Уменьшает к в раз;
- •2. Стабилизирует коэффициент усиления при изменении параметров транзисторов, снижает уровень нелинейных искажений;
- •3. Последовательная оос увеличивает rвх, оос по u уменьшает rвых. Оос нашла преимущественное применение в усилителях
- •2.2.3 Усилители постоянного тока
- •При изменении знака Uвх должен измен. Знак Uвых
- •2 И 3 требование выполняется при работе усилителя в режиме а
- •1 Условие – необходимо отделить полезный сигнал от u питания.
- •1. Упт с одним источником питания
- •Дрейф нуля в упт
- •Борьба:
- •Стабилизация Uпит, стабилизация температуры режима работы, тренировка транзисторов.
- •Использование дифференциальных (балансных) упт.
- •Преобразование усиливаемого напряжения. Дифференциальный упт (балансный)
- •2.2.4 Операционные усилители.
- •Условное обозначение
- •2.2.4.2 Примеры схем на оу:
- •Инвертирующий усилитель
- •7. Дифференцирующий усилитель.
- •2.2.5 Генераторы гармонических колебаний(аг).
- •2 Условие – условие баланса амплитуд
- •3) Аг с кварцевой стабилизацией используют в качестве резонатора пластину кварца
- •Может быть использован как с или l. Можно включить в цепь пос как послед. Колебательный контур.
- •2.2.6 Выпрямители
- •2.2.6.1 Схема однополупериодного однофазного выпрямителя
- •2.2.6.1 Двухполупериодный выпрямитель мостового типа
- •2.2.6.3 Двухполупериодные выпрямители со средней точкой
- •2.2.6.4 Сглаживающие фильтры
- •2.2.6.5 Емкостные фильтры
- •2.2.6.6 Индуктивные фильтры
- •2.2.6.8 Стабилизаторы u и I
- •Промышленностью выпускается в интегральном исполнении -компенсационные стабилизаторы непрерывного действия серии к142
1.1.7. Основные законы электрических цепей.
Соотношение между ЭДС, токами, напряжениями и сопротивлениями подчиняются закону Ома, первому и второму законам Кирхгофа.
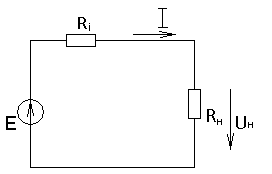
Рис.1.13. Схема замкнутой цепи, содержащей источник ЭДС.
Закон Ома: ток в замкнутой неразветвленной электрической цепи прямо пропорционален ЭДС и обратно пропорционален полному сопротивлению: (рис.1.13)

Закон Ома для участка цепи: падение напряжения на участке цепи пропорционально силе протекающего тока и сопротивлению этого участка:
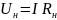
1-й закон Кирхгофа:
Алгебраическая сумма токов в узле электрической цепи равна нулю.
Т.е. для узла а (рис 1.14)

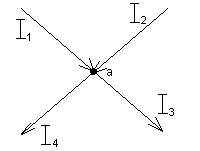
Рис.1.14 узел электрической цепи
При составлении уравнений по первому закону Кирхгофа токи, втекающие в узел, записываются со знаком «+», а вытекающие из узла – со знаком «-».
2-й закон Кирхгофа:
В замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на всех сопротивлениях контура.
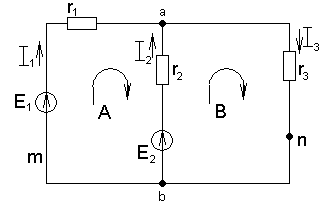
Рис.1.15. Схема сложной двухконтурной цепи.
Для контура авm: (рис. 1.15.)

Для контура аnв:

На рис.1.15. стрелками А и В указаны произвольно выбранные направления обхода контуров. При составлении уравнений по 2-му закону Кирхгофа ЭДС в левой части записываются с «+», если их направление совпадают с направлением обхода контура, и с «-», если они противоположны; падения напряжения в правой части записываются с «+», если направления токов совпадают с направлением обхода, и с «-», если они противоположны.
Падения
напряжений
 в правой части уравнений (по 2-му закону
Кирхгофа) могут быть заменены
соответствующими напряжениями
в правой части уравнений (по 2-му закону
Кирхгофа) могут быть заменены
соответствующими напряжениями
 ,
причем правила знаков остаются теми
же.
,
причем правила знаков остаются теми
же.
Аналогично в правую часть могут быть занесены и иные внешние напряжения или они заменяются ЭДС с противоположным направлением и нулевым внутренним сопротивлением, тогда они учитываются в левой части уравнения ( рис.1.16.)
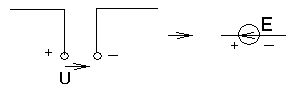
Рис.1.16
Замена
внешнего напряжения эквивалентным
источником ЭДС с
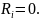
Лекция №2
1.1.8. Эл. Энергия и мощность в цепях постоянного тока
В цепях постоянного тока эл. энергия, вырабатываемая источниками, равна энергии, потребляемой приемниками.
Резистивные
элементы преобразуют эл. Энергию в
тепловую, по закону Джоуля-Ленца энергия,
потребляемая резистивным элементом
сопротивление которого
 в течение времени t
при протекании тока
равна
в течение времени t
при протекании тока
равна


Мощность – это энергия, потребляемая в единицу времени
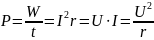

1.1.9 Простые эл. Цепи с последовательным соединением приемников
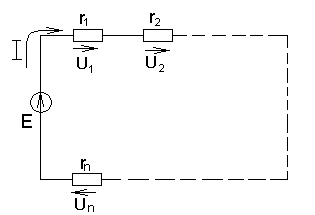
Рис.1.17. Схема цепи с последовательным соединением приемников.
Для этой цепи уравнение по второму закону Кирхгофа
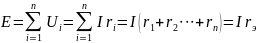
Отсюда
 ;
;
 ;
;
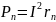
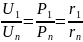
В последовательной цепи падения напряжения и мощности распределяются пропорционально сопротивлениям этих участков.
Такое соединение в промышленных энергосетях используется редко, т.к. при этом невозможна независимая коммутация приемников.
Отказы типа «обрыв» приводят к отключению всех приемников.
Отказы типа «короткое замыкание» отдельного приемника здесь практически не опасны.
1.1.10. Простые эл. Цепи с параллельными соединением приемников.
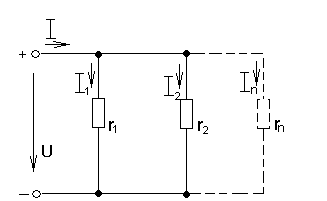
Рис.1.18. Схема цепи с параллельным соединением приемников.
Для этой цепи уравнение по первому закону Кирхгофа

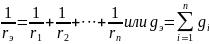

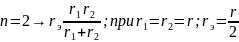
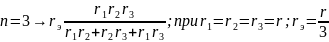
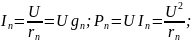

Т.е. в параллельной цепи токи и мощности распределяются по ветвям обратно пропорционально их сопротивлениям.
Здесь допустима независимая коммутация приемников; «обрыв» не влияет на остальные ветви.
1.1.11. Простые эл. цепи со смешанным соединением приемников.
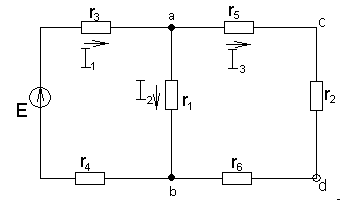
Рис.1.19. Схема цепи со смешанным соединением приемников.
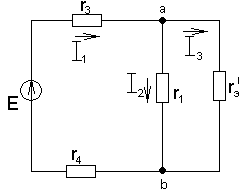
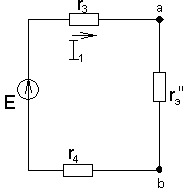
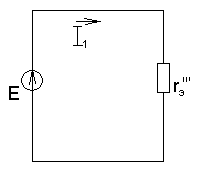
а) б) в)
Рис.1.20. Последовательное свертывание схемы рис.1.19.
 (рис.1.20,а)
(рис.1.20,а)

 (рис.1.20,в)
(рис.1.20,в)



1.1.12. Электрические цепи, содержащие соединения приемников
треугольником и звездой.
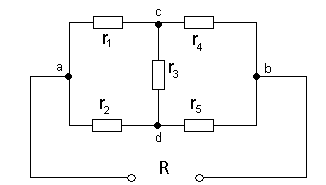
Рис.1.21. Схема эл. цепи, содержащей соединения сопротивлений треугольником и звездой.
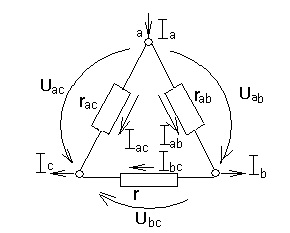
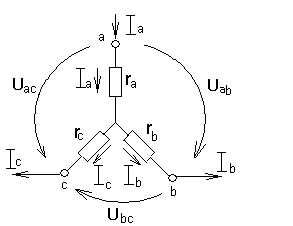
а) б)
Рис.1.22. Замена треугольника эквивалентной звездой.
Эквивалентное
преобразование состоит в том, что после
замены
 в звезду
в звезду
![]()
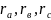 или наоборот токи
или наоборот токи
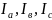 и напряжения
и напряжения
 должны оставаться неизменными.
должны оставаться неизменными.
Для схемы (рис.1.22,а) по второму закону Кирхгофа

А по первому закону Кирхгофа для узла а:

Для узла в:
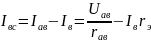

Для схемы (рис.1.22,б) по второму закону Кирхгофа
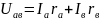
Из
этих уравнений следует:

![]()
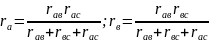

Формулы
обратной замены