1.3.1. Последовательный колебательный контур. Резонанас напряжений.

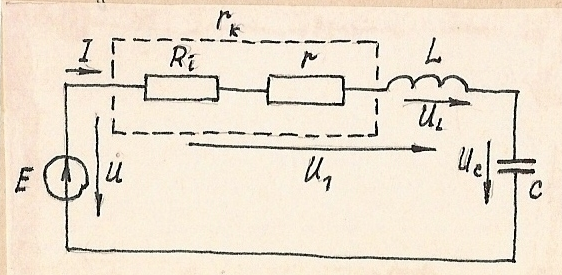
Рис.1.69. Последовательный колебательный контур.

Заменим последовательное соединенные сопротивления R(i) + r сопротивлением r(k)=R(i)+r.

Тогда комплекс полного сопротивления этой цепи:

Рис.1.70. Зависимость реактивных сопротивлений от частоты

На частоте

Частота резонанса:

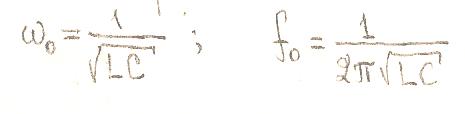
Характеристическое сопротивление контура:

Добротность контура:

Чем меньше активное сопротивление контура r(k), тем выше его добротность.

С другой стороны :

Добротность равна отношению (при резонансе) реактивной мощности в контуре (Q(lk)рез или Q(ck)рез) к активной мощности, поглощаемой контуром.

Полное сопротивление контура при резонансе Z=r(k), т.е. оно становится минимальным и чисто активным:

При этом ток в контуре при резонансе:

Не зависит от величин Х(l) и X(c), и если Р>r(k), то при резонансе ток в контуре резко возрастает.

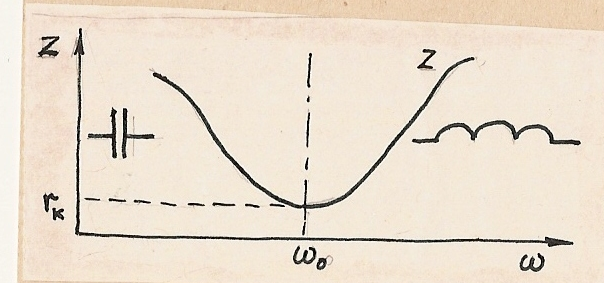
Рис.1.71. Зависимость модуля полного сопротивления последовательного контура опт частоты .

На частоте резонанса: -

При реактивное сопротивление контура носит индуктивный характер, а при -емкостной.

При резонансе в последовательном контуре напряжение на реактивных элементах U(l),U(c) в Q раз превышают напряжение источника U, поэтому резонанс в этом контуре называется резонансом напряжений:

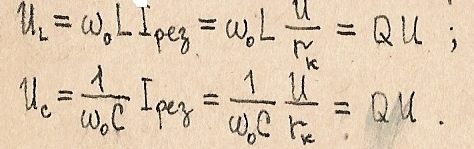
Физически это объясняется колебаниями реактивной энергии в контуре от L к C и обратно. Обмен энергией между источником и контуром не происходит. Ток в цепи обусловлен только активной мощностью.

Представим ток в контуре в колебательной форме:

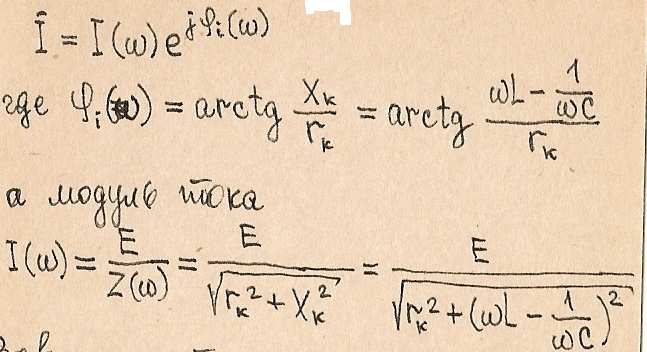
Зависимость модуля тока от частоты при постоянных L,C,r,E называется резонансной характеристикой (резонансной кривой).

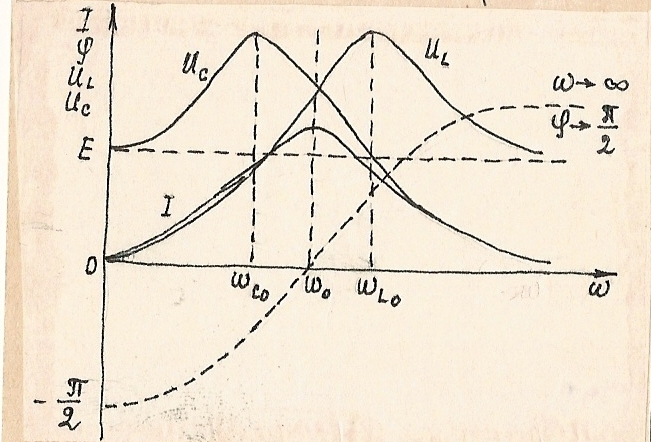
Рис.1.72. Резонансная кривая последовательного контура здесь показаны зависимости тока I, фазового сдвига тока относительно ЭДС Е, напряжений на катушке индуктивности U(l) и на конденсаторе U(c) от частоты ω.

Максимум напряжений на L и C достигается на частотах отличных от резонансной частоты ω◦L Действительно,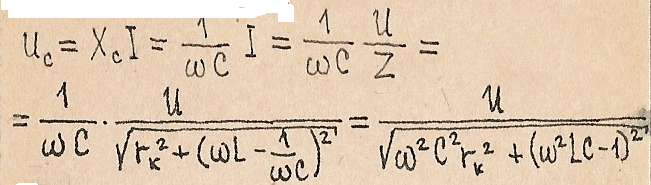

Наибольшее значение U(c) достигается ког7да знаменатель этого выражения минимален. Для определения экстремума приравняем к нулю производную от подкоренного выражения:

Отсюда определяем: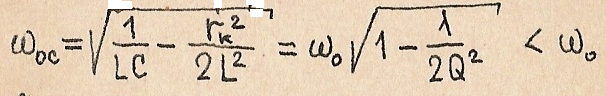

Аналогично определяем: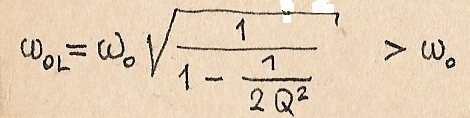

Рассмотрим обобщенную резонансную кривую контура. Пусть у- относительная величина, равная отношению модуля тока на любой частоте к его max значению

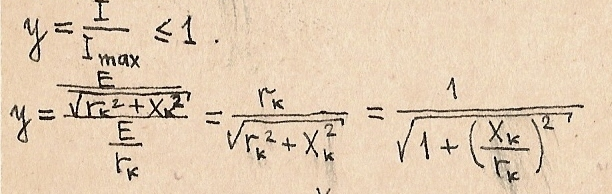
Отношение называется обобщенной расстройкой контура.

Тогда:

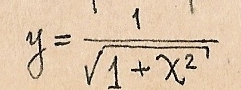
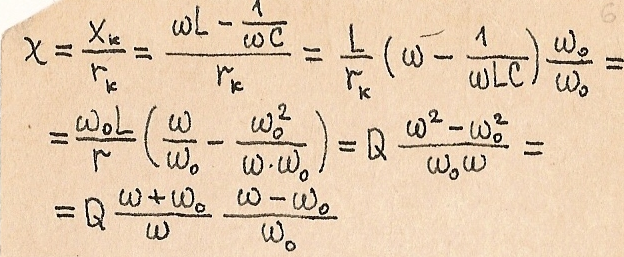
Если расстройка мала, т.е. то

Обозначим -абсолютная расстройка

Тогда:

Где - относительная расстройка

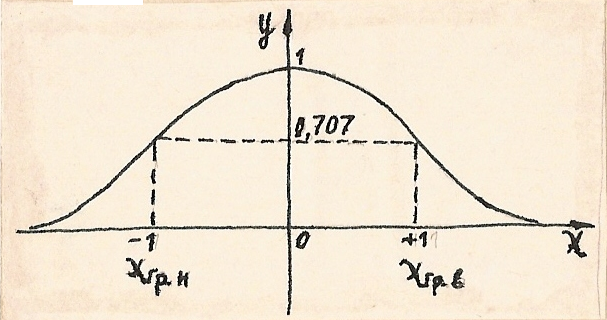
Рис.1.73. Обобщенная резонансная кривая контура:

Значения обобщенной расстройки, при которых у уменьшается в раз,

Так как , то при λ=1

Диапазон частот 2∆ω в котором 1>y>0,707I(ω) ток I(ω) уменьшается до уровня 0,707 I(ω◦) наз. Полосой пропускания контура . Чем больше Q, тем меньше 2∆ω.

Для регулировки резонансной частоты контура Сr.e. для его перестройки

Необходимо изменить L или С.

Известно, что

Отсюда видно, что при увеличении L добротность Q возрастает, а при увеличении С – падает.

1.3.2. Параллельный колебательный контур. Резонанс токов.

Параллельный колебательный контур (элементы L и С включены параллельно источнику ) показан на рис.1.74.

Комплекс полного сопротивления контура:

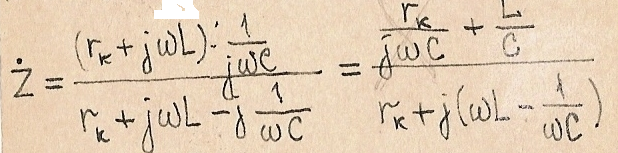
Для обеспечения резонансных свойств контура r(k) должно быть малым, поэтому слагаемым r(k)/jωC в числителе можно пренебречь

При резонансе поэтому сопротивление параллельного контура на частоте резонанса

Возрастает до максимума и становится чисто активным, что подтверждается векторными диаграммами токов при

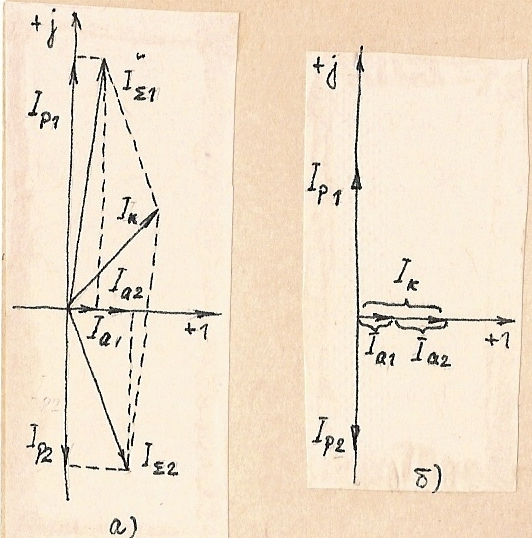
Рис.1.75. Векторные диаграммы токов для параллельного контура:

а) при отсутствии резонанса;

б) на частоте резонанса;

Активные составляющие токов I(a1),I(a2) в ветвях контура значительно меньше реактивных, т.к. проводимости значительно меньше реактивных.

При резонансе, когда и реактивные составляющие токов взаимно компенсируются и ток контура становится минимальным.

Зависимость Z(ω) для параллельного контура приведена на рис.1.76. На частоте Z=R(oe). При реактивное сопротивление контура носит емкостной характер, а при -индуктивный.

Рис.1.76. Зависимость модуля полного сопротивления параллельного контура опт частоты Z(ω).

При резонансе в параллельном контуре ток в реактивных элементах в Q раз превышает ток в цепи источника, поэтому резонанс в этом контуре называется резонансом токов.

Действительно, при и

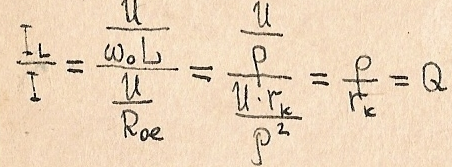
В энергетических цепях явления резонанса токов и напряжений недопустимы,

т.к. приводят к перегрузке элементов.

Колебательные контуры применяются в электронике и радиотехнике (в автогенераторах, радиоприемниках устройствах, избирательных фильтрах и т.д.).

Лекция №8