1.2.9 Цепь синусоидального тока с реальной катушкой индуктивности

Рис 1.57 цепь sin тока с реальной катушкой

индуктивности

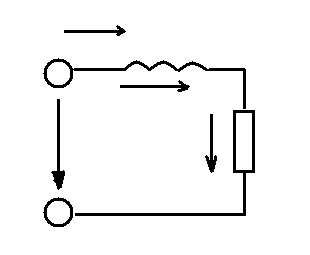
В реальной цепи активное сопротивление катушки и проводов учтено резистором r ( рис. 1.57)

Пусть ток в цепи изменяется по sin закону

I = I_M sin (ωt+ψ_i)

Согласно второму закону Кирхгофа для мгновенных значений напряжения

U = U_L + U_R

Переходя к комплексам напряжений, получаем:

Ù = Ù_R + Ù_L = r Ì + j x_L Ì =Ì (r + jx) = Ì Ż

Где Ż- r + jx комплекс полного сопротивления цепи Z= - его модуль

_L = arctg x_L/r - его фаза; Ż = Z e^{j L} показательная форма записи полного сопротивления.

По закону Ома в комплексной форме Ì = Ù / Ż, или для модулей I = U / Z

Получаем где Ù = Ì Ż = I e ^jψi Z e^{j L} =U e ^jψu, ψ_U = ψ_I + φ_L ; φ_L = ψ_U - ψ_I

Переходя к мгновенным значениям u =U_M sin (ω t+ ψ_i + φ_L)

Следовательно в цепи содержащей последовательное соединение L и r, синусоида напряжения на входе в цепи (т.е суммарного напряжения) опережает по фазе синусоиду тока на угол сдвига тока на угол сдвига фаз φ_L (комплекс суммарного напряжения опережает тока на угол сдвига фаз φ_L )

(рис. 1.58)

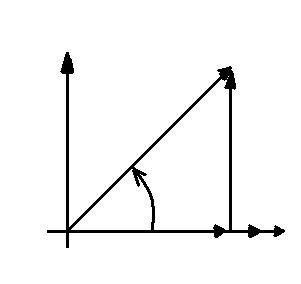
Рис. 1.58 векторная диаграмма с реальной катушкой индуктивности.

Векторная диаграмма строится следующим образом: по оси в выбранных масштабах откладывают вектор тока Ì (по условию ψ_i=0) совпадающий с ним по фазе вектор напряжения на резисторе r: Ù_R =r Ì

Из конца вектора Ù_R параллельно оси 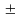j вверх в том же масштабе, что и Ù_R откладывают вектор напряжения на индуктивном элементе L: Ù_R = j x_L Ì

Из начало координат под углом φ_L откладывают отрезок, равный модулю суммарного напряжения Ù = Ì Ż т.е строят вектор напряжения Ù.

Его конец должен совпадать с концом вектора Ù_L т.к по 2 закону Кирхгофа Ù = Ù_R + Ù_L

При выполнения условия совпадения конца вектора суммарного напряжения с концом последнего вектора напряжения участка цепи говорят, что многоугольник напряжений, действующих в цепи, замкнут

Tg φ_L = x_L/r или cos φ_L = r/z

мгновенная мощность при ψ_i=0 (рис. 1.59)

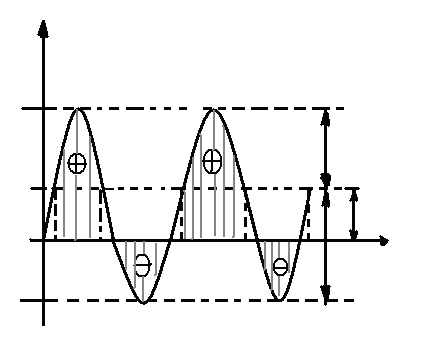
Рис 1.59 график изменения мгновенной мощности в цепи реальной катушкой индуктивности.

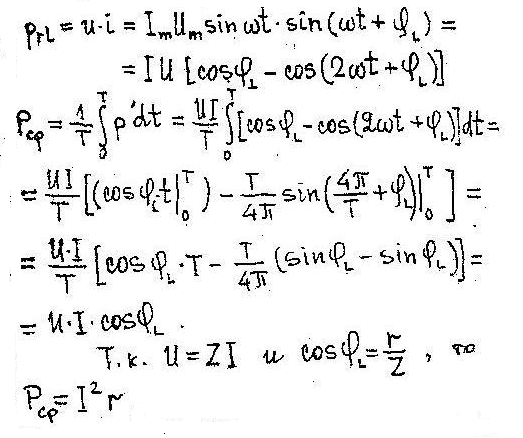
т.е среднее значение мощности в цепи с реальной катушкой индуктивности равно активной мощности ( выделяемой на резисторе r) .

Амплитуда колебания мощности относительно Р_ср называется полной мощностью цепи, В*А (это наибольшее значениe активной мощности которое может быть получено при данных значениях напряжения и тока):

S = U I [B A]

Pеактивная индуктивная мощность катушки.

Q_L = X_L I² = U_L I

Из векторной диаграммы (рис. 1.58) следует:

Ur = U cosφ_L

U_L=U sinφ_L

поэтому:

Q_L= U_L I = U I cosφ_L = S cosφ_L

P = S cosφ_L

P = U_RI = U I cosφ_L = S cosφ_L

P² + Q² = (U I cosφ_L)² + (U I sinφ_L)² = (U I)² = S²

S =

Еще раз подчеркнем что мощность Р является средней мощностью преобразования электроэнергии в другие виды энергии, а реактивная мощность Q характеризует амплитуду колебаний мощности при обмене энергии между источником и магнитным полем катушки.

Введем понятие коэффициента мощности cosφ_L = P / S.

Который характеризует соотношение между активной и реактивной (в данном случае – индуктивной ) мощностями, т.е показывает, какую часть полной мощности цепи составляет активная мощность. Представим активную и полную мощности в комплексной форме:

Ŝ = P + jQ_L = S cosφ_L + jS sinφ_L

Перейдем к показательной форме на основании подстановки Эйлера:

Ŝ = S e ^jφL Ŝ = U I e ^{j (ψu -ψ I)} = U e ^{j ψu} I e -^{j ψ I} = U I

Следовательно для получение полной мощности в комплексной форме необходимо комплекс напряжения умножить на сопряженный комплекс тока:

Ŝ = U I = U e ^{j ψu} I e -^{j ψ I} = S e ^jφL = P+ j Q

Лекция №7

1.3. Резонанс в цепях sin тока. Колебательный контур.

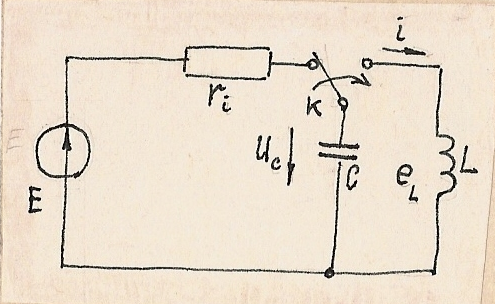
Рис1.68. К возникновению колебаний в идеальном LC-контуре

Предположим, конденсатор С (рис.1.58), подключенный через ключ К к источнику Е, зарядился до напряжения U(l)>0. Энергия запасенного в нем электрического поля:

При переключении ключа К к заряженному конденсатору С подключается катушка индуктивности L и образуется замкнутый контур.

Ток в контуре нарастает постепенно, т.к. его увеличению противодействует ЭДС самоиндукции :

По мере возрастания тока в катушке запасается энергия магнитного поля :

Когда конденсатор разрядится , ток в контуре поддерживает ЭДС самоиндукции до момента, пока энергия запасенного магнитного поля катушки не уменьшится до нуля.

Этот ток заряжает емкость до U(c)<0. описанный процесс повторяется. Замкнутый контур с элементами L и C называется Колебательным.

В идеальном колебательном контуре отсутствуют активные потери, поэтому в нем происходят незатухающие колебания.

В реальном контуре есть активные потери и поэтому возникающие колебания постепенно затухают.

При подключении колебательного контура к источнику гармония. ЭДС в нем при определенных условиях возникают резонансные явления.

Возможны два вида резонанса: при последовательном соединении элементов контура и источника – резонанс напряжений; при параллельном соединении элементов контура и источника – резонанс токов.