1.2.3. Действующее значение синусоидальных эдс, тока и напряжения.

Мгновенное значение синусоидального тока:

i=I_msin(ωt+Ψ_i)

П ри ωt+Ψ_i)=π/2 i=I_m

где I_m – максимальное (амплитудное) значение тока.

Расчёт электрических цепей переменного тока с использованием мгновенных значений ЭДС, тока и напряжения сложны.

Поэтому непрерывно изменяющиеся ЭДС, u, i заменяют эквивалентными постоянными во времени величинами, что упрощает расчёты и позволяет сократить форму записи соответствующих величин.

Действующим (эффективным) значением переменного тока называется такое значение постоянного тока, когда на сопротивлении r за время, равное периоду Т переменного тока, выделиться то же количество энергии, что и на переменном токе.

Энергия, выделяемая постоянным током:

W=I²rT; I – действующие значение синусоидального тока.

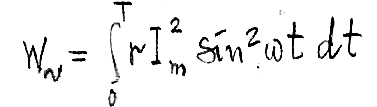Энергия, выделяемая синусоидальным током:

Резистивный элемент

Параметр резистивного элемента – его активное сопротивление r.

Активное сопротивление проводника переменному току превышает его сопротивление постоянному току. Это объясняется неравномерным распределением тока по сечению проводника (так называемый поверхностный эффект): плотность тока на поверхности проводника больше, чем на оси.

Вследствие этого потери энергии на нагрев при переменном токе возрастают. Сопротивление проводника, характеризующее эти потери, увеличивается.

Однако для частоты сетевого тока это увеличение незначительно и в дальнейшем не учитывается.

Мгновенная мощность резистивного элемента

P_r=i²r

не зависит от знака тока и всегда положительна, т.е. в резистивном элементе при переменном токе вся поступающая энергия преобразуется в тепловую.

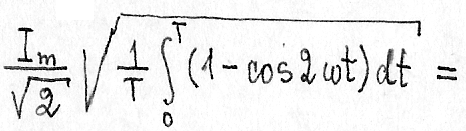Прировняем эти энергии и полученное уравнение решим относительно действующего значения тока с учётом ω=2π/Т:

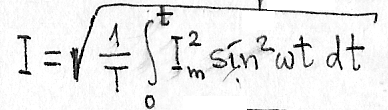
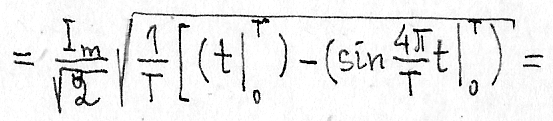
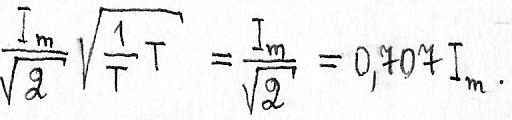
Здесь использовано соотношение:

s in² ωt=1/2(1-cos 2ωt)

Таким образом, действующее значение меньше амплитудного в раз. Аналогично:

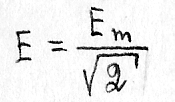
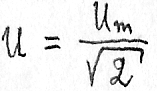
Когда говорят о величинах Е, u, I (без индексов) что имеют в виду действующее значение шкалы измерительных приборов, предназначенных для измерения переменных токов проградуированных в действующих значениях.

В некоторых случаях (например при анализе выпрямителя) пользуются средним значением u, i, под которым понимают среднее арифметическое соответствующей величины за время T/2 (т.к. среднее значение синусоидальной величины за период Т равно 0).

К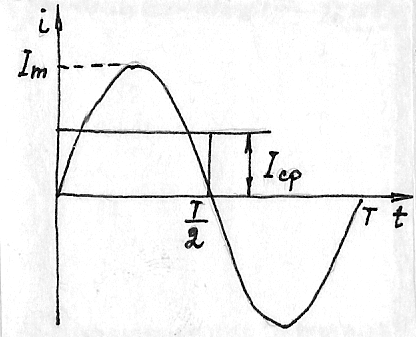 определению среднего значения синусоидального тока.

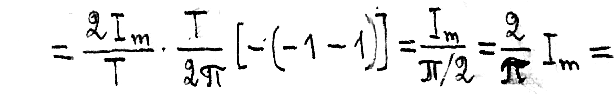
Физический смысл: среднее значение синусоидального тока за время Т/2 характеризует количество электричества, протекающего в цепи за пол-периода.

Аналогично:

Е_ф=2/π Е_m ; u_u=2/π u_m

Отношение действующего значения к среднему называется коэффициентом формы кривой, который характеризует степень искажения синусоиды

K_ф.к=I/I_ср=1,11

4. Методы описания и представления синусоидального тока, эдс и напряжения

П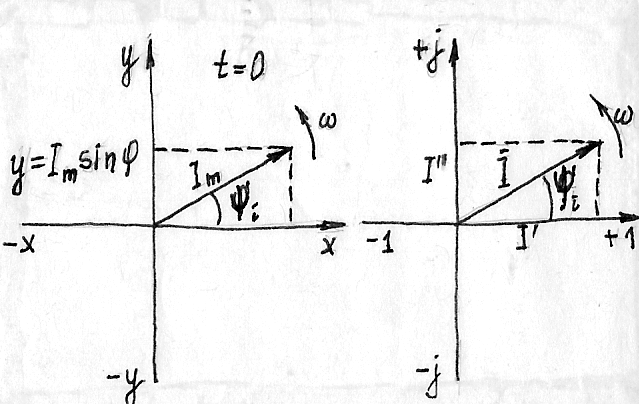 редставление синусоидального тока в виде вращающегося вектора:

а) декартова плоскость;

б)комплексная плоскость.

Синусоидальные токи, ЭДС и напряжения можно описать с помощью тригонометрических функций, изобразить графически в виде временной диаграммы синусоиды и представить в виде вращающихся векторов на декартовой и комплексной плоскостях.

Как известно, синусоидальный ток может быть описан тригонометрической функцией:

i=I_msin(ωt+Ψ)

При представлении синусоидальных величин в виде вращающихся векторов на плоскости декартовых координат:

• Вектор, соответствующий в выбранном масштабе амплитудному значению синусоидальной величины (E_m, u_m, I_m), вращается с угловой частотой, равной угловой частоте ω против часовой стрелки;

• Начальная фаза отсчитывается от положительного направления оси абсцисс также против часовой стрелки;

• Проекции вращающихся векторов на ось ординат равны мгновенным значениям синусоидальных величин.

Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, называются векторной диаграммой.

Применение векторных диаграмм при анализе и исследовании цепей переменного тока позволяет наглядно представить рассматриваемые процессы, а также рассчитать цепь.

При этом для получения суммы или разности ЭДС, u, I используются правила сложения или вычитания векторов.

Недостатком таких расчетов является невысокая точность.

При представлении синусоидальных ЭДС, u, I в виде аналогичных вращающихся векторов, на комплексной плоскости позволяет выразить геометрические операции с векторами переменных токов и напряжений в алгебраической форме, что повышает точность расчётов и обеспечивает возможность применения для расчёта цепей синусоидального тока.

При изображении синусоидальных величин в виде вращающихся векторов на комплексной плоскости ось абсцисс заменяют осью действительных (вещественных) чисел, а ось ординат - осью мнимых чисел;

• Вращающийся вектор, соответствующий в выбранном масштабе действующему значению синусоидальной величины, изображают аналогично тому, как это производилось на плоскости декартовых координат;

• Вектор, обозначенный I, раскладывают на составляющие по оси действительных I` и оси мнимых I`` чисел;

• С 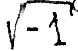оставляющую по мнимой оси выделяют множителем j

j= - мнимая единица.

[В отличие от принятого в математике обозначения мнимой единицы через i в электротехнике применяют обозначение j , чтобы различать с обозначением мгновенного значения тока i ].

Алгебраическая форма записи:

i=I`+jI`` - комплекс тока.

Показательная форма записи:

i=Ie^jΨ

г де I=> модуль комплекса тока.

Ψ=> фаза комплекса тока

Ψ=arctg I``/I`

Тригонометрическая форма записи получается преобразованием показательной формы на основании формулы Эйлера:

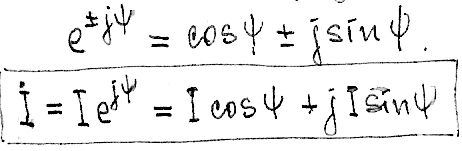
Кроме того, будут использоваться следствия из формулы Эйлера:

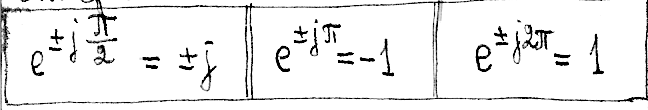
1.2.5 Закон Ома в комплексной форме для цепи с резистивным элементом.

i

u_r

u_R

r

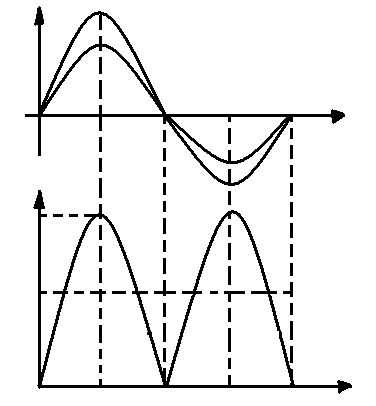
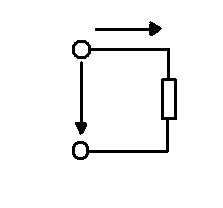
Рис.1.49. Цепь синусоидального тока с резистивным элементом: а) схема; б) временные графики мгновенных значений U_r, i, P_r .

Пусть на вход цепи с активным сопротивлением (резистивным элементом ) рис.1.49, а подано напряжение синусоидальной формы

U_R = U_RM sin (ωt+ψ_U)

Необходимо установить, как изменяются ток і в цепи и мощность P_R, выделяемая на сопротивления r. Согласно закону Ома для мгновенных значений u и i

I = U_R/r = U_RM/r sin (ωt+ψ_U ) = I_M sin (ωt+ψ_I)

где I_M = U_RM/r - амплитуда тока. Для действующих значений I = U_R/r

ψ_U = ψ_I = ψ т.е формы u и i совпадают.

Мгновенные значения мощности

P_R=U_R i=i²r

знака не из меняют, т.е всегда положительный.

Пусть ψ=0, тогда (см. рис 1.49.в)

P_R = U_R I = U_RM I_M sin²ωt = U_RM I_M ½ (1-cos2 ωt) =

= U_RM / * I_M / (1- cos2 ωt) = U_R I - U_R I cos2 ωt

P_R.MAX = 2U_RI

P_R.CP=1/T _R dt = 1/T _R I dt – 1/T _R I cos2 ωt dt =

U_R I - U_R I / T sin (4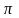 /T)t |^t₀ = U_R I = I² r

т.е средняя мощность равна произведению действующих значений напряжений u тока.

Изобразим рассматриваемые синусоидальные величины на комплексной плоскости, полагая ψ_U=ψ_I=ψ и t=0 (рис.1.50)

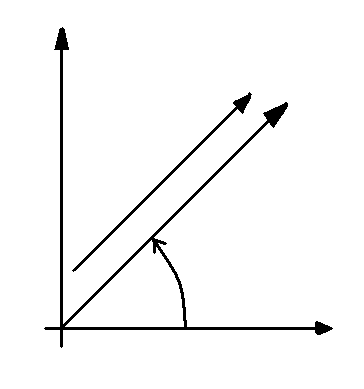Рис.1.50 векторная диаграмма

для цепи синусоидального тока

с резистивным элементом.

Напряжения Ù_R = U_R e ^jψ; ток İ = Ů_R/r = U_R/r e ^jψ = I e ^jψ ;

выражения İ = Ů_R/r

представляет собой запись закона Ома в комплексной форме для цепи с резистивным элементом.

1.2.6. Закон Ома в комплексной форме для цепи с идеальной катушкой индуктивности.

Предположим, что в цепи с катушкой индуктивности активное сопротивление катушки r_L=0 и активное сопротивление подводящих проводов r_пр = 0. Такой случай является идеальным (рис.1.51а).

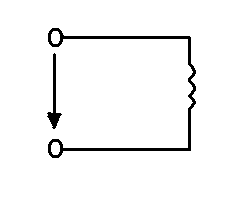
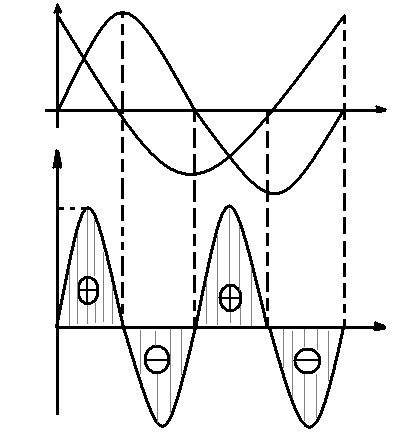
Рис. 1.51 Цепь синусоидального тока с идеальной катушкой индуктивности: а) схема; б) временные графики мгновения значений u_L , i, p_L.

Пусть в этой цепи протекает синусоидальный ток

I = I_M sin (ωt+ψ_i)

тогда мгновенное напряжение катушке

u_L = -e_L = L di/dt = ω L I_M cos (ωt+ψ_i) = U_LM sin (ωt+ψ_i + /2) (1.11)

где U_LM = ω L I_M

Из (1.11) следует, что синусоида напряжения на идеальной катушке индуктивности опережает по фазе синусоида тока на угол сдвига фаз /2. (рис. 1.51б).

Изобразим рассматриваемые синусоидальные величины на комплексной плоскости, перейдя к действующим значениям (рис. 1.52):

Рис. 1.52 векторная диаграмма для цепи sin тока с идеальной катушкой индуктивности

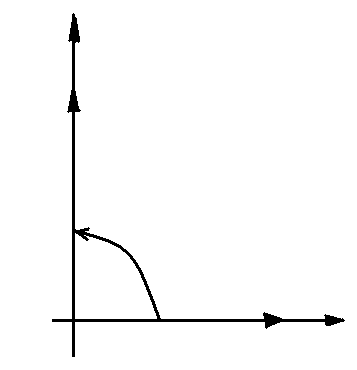
Ì = I e ^jψi ;

Ù_L = U_L e ^{j (ψ}_i^{+ /2)} = ω L I e ^jψ_i e ^{j /2} = jω L I e ^jψi = j ω L Ì = j x_L Ì , (1.12)

где x_L = ωL -модуль активного сопротивления катушки [ c^-1Oм*c = Oм]

j x_L – комплекс индуктивного сопротивления.

На основании выражения (1.12) ранее сформулированное правило о фазовом соотношении тока и напряжения в цепи с идеальной катушкой индуктивности сводится к следующему:

-вектор напряжения на идеальной катушке индуктивности опережает по фазе вектор тока на угол сдвига фаз π/2.

Закон Ома в комплексной форме имеет вид

Ì = Ù_L / j x_L или для модулей: I = U_L / x_L.

Мгновенное значения при ψ_I = 0

p_L =u_L I = U_LM I_M sin (ωt+ /2) sin ωt =

= U_LM I_M 1/2 [ cos /2 –cos(2ωt + /2­) ] =

= - U_L I cos (2ωt + /2­) = x_L I² sin ωt

Следовательно, мгновенная мощность имеет амплитудное значениe x_L I² и изменяется с данной частотой 2ω (рис.1.51.б)

В первую четверть периода u_L > 0 , I > 0, p_L> 0, энергия источника переходит в энергию магнитного поля катушки индуктивности. Максимальное значение накопленной энергии

W_L = ½ L I²_m

Во вторую четверть периода u_L < 0 , I > 0, p_L < 0, энергия магнитного поля катушки возвращается и источник. Cредняя мощность за период

P_L.CP = 1/T _L dt = 0

Таким образом, в цепи с идеальной катушкой индуктивности непрерывное колебание (обмен) энергия между источником и магнитным полем катушки без затрат энергии источника.

Амплитуда колебаний мощности в цепи с идеальной катушкой называется реактивной индуктивной мощностью;

эта мощность, обусловлена энергией магнитного поля индуктивности;

единица измерения – вар – вольт - ампер - реактивности.

Q_L = U_LI = X_LI²

1.2.7 Закон Ома в комплексной форме для цепи с идеальным конденсатором.

Идеальный конденсатор не имеет активных потерь. Предположим, что активное сопротивление конденсатора r_S= , а активное сопротивление подводящих проводов r_пр=0.

Цепь с идеальным конденсатором показана на рис. 1.53.а

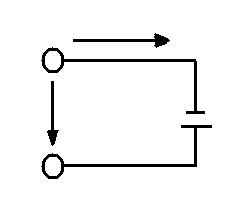
Рис. 1.53 Цепь синусоидального тока с идеальным контуром: а) схема; б) временные графики мгновенных значений u_C, i, p_C .

Пусть в этой цепи действует синусоидальное напряжение

u_C =U_CM sin (ωt+ψ_u)

Тогда мгновенным значением тока

I =C (du_C/dt) = ω CU_CM cos (ωt+ψ_u) = I_M sin (ωt+ψ_u+ /2) (1.13)

Где I_M = ω CU_CM = U_CM / (1/ω C)

Из (1.13) следует, что синусоида емкостного тока опережает по фазе синусоиду напряжения на кондукторе на угол сдвига фаз π/2 (рис. 1.53.а ).

Изобразим рассматриваемые sin величины на комплексной плоскости, перейдя к действующим значением (рис. 1.54)

Рис. 1.54 векторная диаграмма sin тока

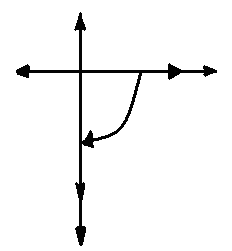
для цепи sin тока с идеальным конденсатором.

Ù_C = U_C e ^jψu

Ì = I e ^{j(ψu+ /2)} = U_C / (1/ω C) e ^jψu e ^{j /2} =

= j U_C / x_C e ^jψu = Ù_C / -jx_C

Для модулей : I = U_C / x_C

Где x_C = 1/ ω C - модуль емкостного сопротивления конденсатора.

Выражения (1.14) представляет собой запись закона Ома в комплексной форме для цепи с идеальным конденсатором. На основании данного выражения ранее сформулированное правило о фазовом соотношении тока и напряжения в цепи с идеальным конденсатором сводится к следующему: -вектор тока в цепи с идеальным конденсатором опережает по фазе вектор напряжения на углом сдвига фаз π/2 . Mгновенное значение мощности при ψ_U = 0

p_C = u_C I = U_CM I_M sin ωt sin (ωt+ /2) = U_CM I_M ½ [ cos π/2 – cos(2 ωt+ /2) ] = - U_C I cos (2ωt+ /2) = U_C I sin 2ωt = x_C I² sin 2ωt .

Следовательно, мгновенная мощность имеет амплитудное значения x_C I² и изменяется с двойной частотой 2ω (рис.1.53 а).

В первую четверть периода u_L > 0 , I > 0, p_L> 0, энергия источника переходит в энергию электрического поля конденсатора (конденсатор разряжается )! Max значение накопленной энергии W_C = ½ CU²_CM . Во вторую четверть периода n_C > 0, I < 0, p_C < 0 , энергия электрического поля возвращается в источник (конденсатор разряжается )!

Средняя мощность за период P_С.CP = 1/T _L dt = 0. Таким образом, в цепи с идеальным конденсатором происходит непрерывное колебание (обмен) энергии между источником и электрическим полем конденсатора без затрат энергии источника. Амплитуда колебаний в цепи с идеальным конденсатором называется реактивной емкостью (мощность, обусловленная энергией электрического поля емкости )

Q_С= U_С I= X_СI²

1.2.8 Законы Кирхгофа в комплексной форме для цепей синусоидального тока

Законы Кирхгофа как универсальные законы электрических цепей в цепях переменного тока справедлива для мгновенных значений ЭДС, токов и напряжений. Для цепей sin тока во многих случаях целесообразнее уравнения электрического состояния цепей по законам Кирхгофа записывають в векторной форме.

Первый закон Кирхгофа для цепей sin тока записывается и формулируется так

Ì_K = 0

т.е геометрическая сумма векторов тока ветвей сходящихся в узле, равна нулю.

Узел цепи, в котором сходится токи Ì₁, Ì₂, Ì₃ показана на рис. 1.55а, а векторная диаграмма на комплексной плоскости для токов этого узла на рис 1.55,б

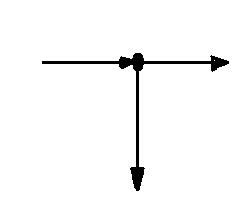
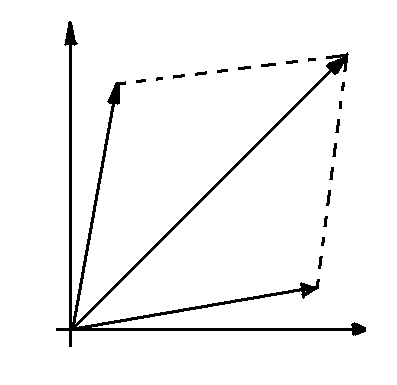
Рис. 1.55 к пояснению I Закона Кирхгофа в комплексной форме а) узел эл. цепи б) векторная диаграмма токов данного узла на комплексной форме

Уравнение по I закону Кирхгофа для этого узла имеет вид Ì₁ - Ì₂ - Ì₃ = 0 или

Ì₁ = Ì₂ + Ì₃ т.е. вектор тока Ì₁ равен векторной (геометрической) сумме векторов токов Ì₂ и Ì₃ (рис.1.55.б)

При представлении sin токов комплексными величинами I закона Кирхгофа формулируется так: алгебраическая сумма значений токов , сходящихся в узле , равно нулю.

Bторой закон Кирхгофа записывается и формулируется следующим образом:

-для замкнутого контура геометрическая сумма векторов эдс , действующих в контуре, равна геометрической сумме векторов напряжений его участков.

B комплексной форме :

-для замкнутого контура алгебраическая сумма комплексов эдс равна алгебраической сумме комплексов напряжений.

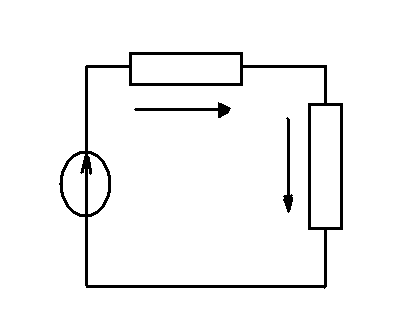
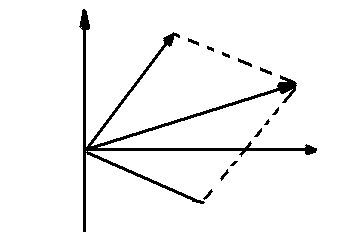
Рис.1.56 к пояснению второго закона Кирхгофа в комплексной форме: а) замкнутый контур электрической цепи; б) векторная диаграмма ЭДС и напряжений данного контура на комплексной плоскости. Уравнение по второму закону Кирхгофа для данной цепи (рис. 1.56.а) имеет вид (рис. 1.56б)

Лекция №6