Аналітична геометрія

1.Види рівнянь прямої лінії на площині.

Озн. Напрямним вектором прямої називається б-я ненульовий вектор колінеарній цій прямій.

Т. Рівняння прямої лінії, яка проходить через задану т. і має напрямний вектор задається формулою: або загальне рівняння прямої.

Т. Довільна пряма лінія на площ задається рівнянням першого степеня, вигляду відносно дек системи координат.

Озн. Загальне рівняння прямої відносно дек системи координат називається повним, якщо , , і неповним в протилежному випадку.

Рівняння прямої у відрізках: де

Рівняння прямої, яка проходить через дані 2 точки: Нехай , , . т. - фіксована.

Параметричні рівняння прямої:

.

Векторне рівняння прямої: де , , .

Рівняння прямої з кутовим коефіцієнтом:

Озн. Кутом нахилу даної прямої до вісі , проти годинникової стрілки навколо точки А до її співпадає з даною прямою. Якщо пряма то відповідний кут нахилу дорівнює 0.

Озн.2 Кутовим коефіцієнтом прямої називається кута нахилу цієї прямої до вісі , тобто .

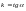Лема. Нехай пряма на площині, яка не паралельна має напрямний вектор , тоді має місце формула: .

Рівняння прямої, що проходить через точку і має кутовий коефіцієнт : . де .

Озн. Рівняння називається нормованим рівнянням прямої, якщо виконуються умова .

2. Види рівнянь прямої лінії в просторі

Т. Рівняння прямої, яка проходить через т. і має напрямний вектор таке: .

Параметричні рівняння прямої:

Векторне рівняння прямої:

де , .

Рівняння прямої в просторі, що проходить через дві задані точки:

, ,

Пряма лінія, як перетин двох площин:

3.Взаємне розміщення прямих у просторі заданих своїми канонічним рівняннями.

Нехай в просторі задані дві прямі рівняннями:

Т: 1) Для того, щоб прямі І,ІІ були мимобіжними (не лежали в одній площ) щоб виконувалося умова

2) Для того, щоб прямі І, ІІ перетинались щоб , але вектори , були не колінеарними.

3) Для того, щоб прямі І, ІІ були паралельні між собою щоб вектори були колінеарні , але вектор не був колінеарним до цих векторів.

4) Для того, щоб прямі І, ІІ зливались щоб вектори були колінеарні між собою.

4. Канонічне рівняння еліпса. Директриси еліпса та їхні властивості.

Озн. Еліпсом називається геометричне місце точок площини, сума віддалей від яких до двох фіксованих точок площ (фокуси) є величина стала.

Фокуси ,

, .

точка лежить на еліпсі . Отже, рівняння має вигляд: . , , .

Директриси еліпса та їхні властивості.

Нехай - велика піввісь еліпса.

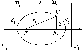Озн. Ексцентриситетом еліпса називається. величина вигляду: 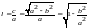(овальність).

Озн. Директрисою еліпса, яка відповідає фокусу називається. пряма лінія, розташована в півплощині перпендикулярно великій вісі еліпса на віддалі від центру симетрії еліпса - початок координат:

Т: Правильними є співвідношення:

.