3. Розклад аналітичних функцій в ряди Тейлора

Нехай задано послідовність функцій , визначених на деякій множині . Тоді вираз

називається функціональним рядом.

Простішим серед функціональних рядів є степеневі ряди, тобто ряди вигляду:

де – фіксована послідовність комплексних чисел, і - комплексна змінна.

Сума степеневого ряду є нескінченно разів диференційованою функцією в крузі збіжності . При цьому для довільного Зокрема, при звідси дістанемо, що ( ), а степеневий ряд можна переписати у вигляді

. Ряд в такому вигляді називається рядом Тейлора функції .

4. Теорема Ліувілля про цілі функції та їх застосування до доведення основної теореми алгебри

Т(Ліувілля) Якщо – аналітична функція в і обмежена там, то вона є сталою.

Справді, якщо – ціла функція і для деякого , то, розвиваючи її в степеневий ряд в околі деякої точки з (бо !), для коефіцієнтів дістанемо:

. Звідси для довільного фіксованого при отримуємо, що , а

Т. (основна теорема алгебри) Кожний многочлен має принаймні 1 нуль.

Справді, якщо це не так (тобто для всіх ), то розглянемо функцію . Вона також є, очевидно, цілою. Крім того, оскільки . Тому для вибраного існує таке , що при виконується нерівність . Для тих , для яких , з деяким , тому, що – неперервна функція на замкненому крузі . Отже, для всіх : і тому за теоремою Ліувілля функція , а з нею й многочлен , повинні бути сталими, що суперечить з припущенням (або ж тому, що з урахуванням співвідношенням функція повинна бути тотожним нулем).

З теореми вже легко дістати, що многочлен –го степеня має в точно коренів (з урахуванням їх кратностей).

Диференціальна геометрія

2. Тригранник Френе Формули Френе

– векторний тригранник Френе

нормаль

спрямна

стична

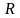
0

, ,

– рівняння дотичної,

– рівняння стичної площини,

– рівняння нормальної площини.

Формули Френе

Це система диференціальних рівнянь :

,

де – кривина лінії

– скрут лінії

– натуральний параметр

– векторний тригранник Френе.

, ,

5. Топологічні відображення та їхні властивості

Нехай задано два топологічні простори та . Розглянемо відображення це відображення називається топологічним, якщо :

а) воно є взаємно однозначним ( , з того що не )

б) неперервне ( неперервне в точці якщо для будь-якої відкритої множини, і для будь-якого околу окіл точки , ).

в) неперервне.

Топологічне відображення встановлює відповідність між топологіями. Для того, щоб відображення було топологічним необхідно і досить, щоб образ відкритої множини була відкрита множина і повний прообраз множини з відкритою в .

Простори та – топологічно еквівалентні і позначаються .

Теореми про існування кривини лінії

Озн. Кривиною кривої, віднесеної до натуральної параметризації називається:

, де – кут між векторами де ,

Теорема: У кожній звичайній точці, – приріст . двічі неперервнодиференційовно кривої існує єдина

0

кривина; якщо крива має параметр , де - натуральний параметр, то кривина цієї кривої

А

М К

В

розглянемо МАВ– рівнобедрений МА=МВ, бо АК=КВ поділимо на . перейшовши до границі при