5. Закон великих чисел.

Теореми, що носять назву закону великих чисел, дають умови збіжності середнього арифметичного ВВ до їх математичного сподівання.

Т1. (закон великих чисел Чебишева). Нехай 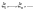– послідовність незалежних ВВ, дисперсія яких обмежена зверху однією і тією ж сталою , тобто . Тоді

Звідси випливає, що .

Т2. (закон великих чисел Пуассона). Якщо у послідовності незалежних випробувань – ймовірність успіху (появи деякої події А в -му випробуванні.), а – число настання події А при випробувань, то

(1)

Звідси випливає, що при оцінці , що

(2)

Заув. Якщо , то з (1), (2) , .

Ці формули є законом великих чисел Бернуллі.

Комплексний аналіз

1. Аналітичні функції: означення, геометричний зміст похідної, умова Коші – Рімана – Ейлера - д’Аламбера.

Якщо є диференційована в кожній точці деякої області , то вона в цій області називається аналітичною.

Функція називається аналітичною в точці, якщо вона диференційована в деякому околі цієї точки.

називається диференційованою в точці , якщо її приріст можна подати у вигляді де - нескінченно мала вищого порядку ніж

Геометричний зміст похідної: умовно можна поділити на дослідження модуля та аргументу похідної. Нехай функція в області є комплексно значна функція, яка має похідну в деякій точці . Нехай де - комплексно значна функція від дійсного аргументу. . Якщо яка в деякій точці : , то в на кривій можна провести дотичну до кривої , яка проходить через точку і утворює кут , тоді якщо аналітична в така , то аргумент похідної можна трактувати, як кут на який потрібно повернути дотичну до деякої кривої , що проходить через , щоб дістати дотичну до образу кривої у відповідній точці . Аналогічно можна отримати, що - це коефіцієнт розтягу векторів .

Т Для того щоб була диференційована в щоб вона задовольняла умови Коші- Рімана-Ейлера-Д’Аламбера (КРЕДо):

1) - диференційовні в точці

2) в цій точці і

При виконанні цих умов похідна від може бути обчислена:

О Функція , яка має в деякій області неперервні частинні похідні до другого порядку включно і задовольняє рівняння Лапласа називається гармонічною.

Виходячи з умов Кредо: ; легко отримати, що тобто аналітичні функції є гармонічними.

2. Інтегральна формула Коші

Нехай функція є однозначна і аналітичною в деякій області , а – така замкнена жорданова спрямлювана крива, що . Якщо одна і та ж точка кривої відповідає двом або більшій кількості значень параметра, з яких принаймні одне відмінне від і , то вона називається кратною. Крива без кратних точок називається простою або жордановою.

Якщо точна верхня межа величин відносно всіляких наборів точок є скінченою, то крива називається спрямлюваною.

Тоді для будь-якої точки справедлива інтегральна формула Коші

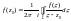
Ця формула дає змогу знайти значення аналітичної функції всередині кривої через її значення на кривій.

Для її встановлення опишемо з точки , як з центра, таке коло радіуса , що

Тоді за теоремою про складений контур

оскільки, очевидно, підінтегральна функція є аналітичною в за винятком, можливо, точки . Зазначимо також, що інтеграл у правій частині останньої рівності за тією ж теоремою про складений контур від не залежить. Тому досить встановити рівність:

або інше граничне співвідношення

. З цією метою оцінимо різницю

Оскільки функція неперервна в точці , то для , що нерівність виконується для всіх , якщо тільки . Тоді для таких значень і отримуємо . Отже, , що і потрібно було довести.

При зроблених припущеннях щодо функції і контуру інтеграл називається інтегралом Коші.