2. Лінійні оператори в лінійних просторах. Матриця лінійного оператора.

Розглянемо - скінчено вимірний лінійний простір . Відображення   векторному простору ставить у відповідність цілком визначений інший вектор цього ж простору: . називається образом вектора а , а називається образом вектора а; перетворення лінійного простору .

Перетворення  простору називається лінійним перетворенням або лінійним оператором , якщо воно задовольняє:

1) ;

2) .

Властивості лінійних операторів:

1) лінійний оператор простору лінійній комбінації векторів простору відображає в лінійну комбінацію k образів із тими ж числовими коефіцієнтами

2) лінійний оператор  простір відображає нульовий вектор простір сам в себе, а протилежний вектор до вектора А в вектор, протилежний його образу: 0=0, .

Т. Для  впорядкованої системи векторів простору  єдиний лінійний оператор  простір , при якому вектор цієї системи є образами деякої бази e, тобто  між лінійним оператором і впорядкованої системи векторів цього просторів є взаємна однозначність відповідність.

Матриця лінійних операторів. Треба знайти матрицю . Образи бази:

;

- матриця лінійних операторів  в базі e; . Щоб знайти А треба помножити  на  вектор бази і одержимо образи векторів бази розкласти за векторами даної бази. Коефіцієнти розкладу – елементи А.

3. Евклідові простори. Ортонормовані бази, їх існування. Процес ортогоналізації.

Нехай – дійсний лінійний простір. В цьому просторі задано правило, за яким  парі векторів ставиться у відповідність дійсне число (a,b)єR.. Це дійсне число називається скалярним добутком векторів a,b, якщо воно задовольняє властивості:

1) ;

2)

3) ;

4)

Дійсний лінійний простір, в якому введено скалярний добуток векторів, називається евклідовим простором і позначається . 1)-4) називаються аксіомами скалярного добутку.

Насл.:

1. ;

2. ;

3.e–база

Два вектори простору називаються ортогональними, якщо їх скалярний добуток дорівнює 0. Система векторів простору називається ортогональною, якщо скалярний добуток  пари векторів дорівнює 0.

Т.  ортогональної системи ненульовий вектор є лінійно незалежний.

Процес орт. – лінійно незалежна не ортогональна система. Побудуємо – ортогональна . При  значенні Припустимо, – лінійно залежні лінійно залежні, що суперечить умові.

підбираємо так, що

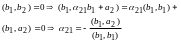
Якщо відомі , то

При  дійсному значенні , бо і протилежному випадку система векторів лінійно залежна.

це буде тоді, коли . Припустимо, що ми побудували систему векторів : . Цей алгоритм побудови системи векторів називається процесом ортогоналізації системи векторів. Вектор називається нормованим, якщо його довжина дорівнює 1. Система векторів називається ортонормованою, якщо вона ортогональна і  її вектор норм. .База e називається ортонормованою, якщо вона ортогональна і  її вектор норм. . В  евклідовому просторі  ортонормовані бази

Тв.

В ОНБ і тільки в ній скалярний добуток дорівнює сумі добутку їх відповідних координат.