Диференціальні рівняння

1. Поняття рівняння, розв’язку, інтеграла. Основні типи інтегральних рівнянь першого порядку. Рівняння з відокремленими змінними, лінійні, в повних диференціалах.

Озн1. Диференціальним рівнянням називається рівняння, в яке входить похідна, або диференціал невідомої функції.

Озн2. Розв’язком диференціального рівняння називається функція, яка має неперервні похідні до порядку та перетворює це рівняння в тотожність.

Озн3. Порядком диференціального рівняння називається найбільший порядок похідної, яка насправді входить в рівняння.

Озн4. Розв’язок в неявній формі будемо називати інтегралом диференціального рівняння.

Озн5. Інтегралом диференціального рівняння називають функцію, яка вздовж будь-якого розв’язку диференціального рівняння є сталою величиною.

І.

– незалежна змінна, – шукана функція; 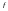– відома функція двох змінних.

І. Рівняння з відокремленими змінними.

, права частина зображається у вигляді добутку функцій однієї змінної. Напр., .

ІІ. Лінійні рівняння.

Лінійним називається рівняння, в якому невідома функція та її похідна входять лінійно, тобто рівняння виду , входять в рівняння лінійно. , (1)

а) Розв’язок шукаємо у вигляді (2)

: . , , , , .

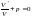
б) . , , .

ІІІ. Рівняння в повних диференціалах.

, явне рівняння 1-го порядку в симетричній формі. Воно називається рівнянням в частинних похідних, якщо його ліва частина є повний диференціал деякої функції двох змінних.

Повний диференціал – головна лінійна частина приросту. . , . , . Отже, існує функція . . , .

2. Формулювання теореми про існування та єдиність розв’язку задачі Коші для рівняння . (Без доведення) . Лінійні диференціальні рівняння -го порядку, поняття про фундаментальну систему розв’язків, вронскіан, конструкція загального розв’язку.

Т. Якщо функція – неперервна, (1) ( - незалежна змінна, - шукана функція, - відома функція) по сукупності змінних , тобто виконуються умови теореми Пеано, а по змінній задовольняє співвідношення:

,

то через кожну точку області проходить єдиний розв’язок рівняння (1).

Т Пеано. Якщо функція неперервна в області , то через кожну точку області проходить хоч один розв’язок рівняння (1), тобто це теорема існування.

Приклад1.

, , функція скрізь визначена.

, , – умова т-ми Пеано виконується. Не виконується умова т-ми Осгуда.

, , ,

– особливий розв’язок.

Т Осгуда. якщо область опукла (будь-які дів точки можна сполучити відрізком, який належить цій області), - приріст функції по другому аргументу:

, а інтеграл не існує , то через кожну точку області проходить не більше одного розв’язку рівняння (1) – теорема єдиності.

Приклад 2. . Функція – неперервна на всій площ. Умова теореми Пеано виконується. Якби мала неперервну похідну по : , тобто виконується умова Ліпшіца.

Якщо , то – диференційована функція, тому виконуються умови Осгуда і Ліпшіца, тобто через кожну точку крім точок осі проходить єдиний розв’язок . Отже, перевірити умову Осгуда потрібно лише при , тоді . Опускаємо модуль: . , , , .

Лінійні диференціальні рівняння -го порядку, поняття про фундаментальну систему розв’язків, вронскіан, конструкція загального розв’язку.

Лінійне рівняння – це рівняння вигляду

(1)

– визначник Вронського (вронскіан) – розв’язки лінійного диференціального рівняння (1). Якщо функції лінійно залежні ( ), то .

Якщо однорідного рівняння (1) , лінійно незалежні, то в жодній точці. Сукупність штук лінійно незалежних розв’язків однорідного рівняння -го порядку , називають фундаментальною системою розв’язків. Якщо – фундаментальна система розв’язків, то вираз типу – загальний розв’язок для рівняння .