
- •Механическое движение тела. Понятие материальной точки. Путь и перемещение тела. Система отсчёта. Относительность механического движения.
- •Виды механического движения тела. Понятие скорости. Ускорение.
- •Вопрос 3
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Закон Гука в простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:
- •Вопрос 8
- •Виды трения
- •Определение коэффициента трения
- •Коэффициент трения покоя
- •Коэффициент трения скольжения
- •Вопрос 9
- •Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость
- •Вопрос 10
- •Механическая работа
- •Абсолютная шкала температур
- •Коэффициент полезного действия тепловых двигателей
- •Эдс индукции
- •Первый закон Кирхгофа.
- •Надо знать !
- •Колебания нитяного маятника
- •Книжная полка
- •Маятник фуко в парижском пантеоне
- •Сделай модель маятника фуко сам !
- •Крутильный маятник
- •Сделай крутильный маятник сам!
- •Знаешь ли ты ?
- •Переменный электрический ток
- •Работа и мощность переменного тока
- •Полосы равного наклона
- •Интерференция от клина. Полосы равной толщины
- •Кольца Ньютона
- •Дифракция на щели [править]
- •Свойства световых лучей. Призматический и дифракционный спектры
Абсолютная шкала температур
Во всех рассмотренных ранее температурных шкалах нуль был выбран произвольно. Такой выбор нуля температур существенно усложняет теоретический вывод ряда зависимостей, приводит к громоздким формулам и ненужным вычислениям.
Исходя из этих соображений, У. Томсон (получивший за научные заслуги титул лорда Кельвина) предложил в 1848 г. ввести новую шкалу температур, которая называется либо абсолютной, либо термодинамической шкалой температур. Температура, измеренная по этой шкале, называется абсолютной температурой (или термодинамической температурой).
Мы знаем, что температура определяется средней кинетической энергией беспорядочного (теплового) движения частиц вещества. В газах это движение молекул или атомов. Введем новую шкалу температур так, чтобы абсолютная температура была пропорциональна средней кинетической энергии беспорядочного движения молекул.
Вспомним, что от средней кинетической энергии молекул зависит давление газа: чем больше кинетическая энергия молекул, тем с большей скоростью и чаще они соударяются со стенками сосуда. Поэтому при неизменном объеме газа и неизменном числе молекул в нем давление газа будет прямо пропорционально его абсолютной температуре
Нам осталось ввести единицу абсолютной температуры и установить нулевой уровень термодинамической шкалы. За единицу абсолютной температуры принят кельвин (1 К); он равен одному градусу Цельсия.
Абсолютный ноль температуры определен экспериментально и равен —273,15 °С. Отсюда следует: температура плавления льда по абсолютной шкале температур равна 273,15 К. Соответственно температура кипения воды равна 373,15 К.
При очень низких температурах наблюдаются необычные явления, в частности сверхтекучесть гелия и сверхпроводимость некоторых металлов. В 1978 г. советский физик П. Л. Капица за исследования в области низких температур был удостоен Нобелевской премии.
При сверхнизких температурах в последние годы получены новые необычные состояния вещества.
Билет 16
Уравнение состояния идеального газа.
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температуройидеального газа. Уравнение имеет вид:
![]() ,
,
где
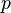 — давление,
— давление, — молярный
объём,
— молярный
объём, — универсальная
газовая постоянная
— универсальная
газовая постоянная — абсолютная
температура,К.
— абсолютная
температура,К.
Так
как ![]() ,
где
,
где ![]() — количество
вещества,
а
— количество
вещества,
а ![]() ,
где
,
где ![]() —
масса,
—
масса, ![]() — молярная
масса,
уравнение состояния можно записать:
— молярная
масса,
уравнение состояния можно записать:
![]()
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
Уравнение,
выведенное Клапейроном содержало некую
неуниверсальную газовую постоянную ![]() ,
значение которой необходимо было
измерять для каждого газа:
,
значение которой необходимо было
измерять для каждого газа:
![]()
Менделеев же обнаружил, что прямо пропорциональна , коэффициент пропорциональности он назвал универсальной газовой постоянной.
Билет 17
Понятие изопроцесса. Основные газовые законы(закон Бойля-Мариотта, закон Шарля, закон Гей-Люссака).
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма иадиабата соответственно. Изопроцессы являются частными случаями политропного процесса
Закон Бо́йля — Марио́тта — один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Описывает поведение газа в изотермическом процессе. Закон является следствием уравнения Клапейрона[1].
Закон Бойля — Мариотта гласит:
При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно.
В математической форме это утверждение записывается следующим образом
![]()
где
—
давление газа; ![]() —
объём газа.
—
объём газа.
Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молярная масса газа, тем больше это отличие.
Закон Бойля — Мариотта, закон Шарля и закон Гей-Люссака, дополненные законом Авогадро, образуют уравнение состояния идеального газа
Зако́н Ша́рля или второй закон Гей-Люссака — один из основных газовых законов, описывающий соотношение давления и температуры для идеального газа. Экспериментальным путем зависимость давления газа от температуры при постоянном объёме установлена в 1787 году Шарлем и уточнена Гей-Люссаком в 1802 году.\
Закон Гей-Люссака — закон пропорциональной зависимости объёма газа от абсолютной температуры при постоянном давлении, названный в честь французского физика и химика Жозефа Луи Гей-Люссака, впервые опубликовавшего его в 1802 году.
Следует отметить, что в англоязычной литературе закон Гей-Люссака обычно называют законом Шарля и наоборот. Кроме того, законом Гей-Люссака называют также химический закон объёмных отношений.
Билет 18
Внутренняя энергия системы. Способы ее измерения. Первый закон термодинамики.
|
Важной характеристикой термодинамической системы является ее внутренняя энергия. Как известно, энергия тела состоит из кинетической энергии движения тела со скоростью v и потенциальной энергии тела во внешних силовых полях (гравитационном, магнитном и т. д.): Eмех=(1/2)·mv2+Eпот. Согласно МКТ, все тела состоят из молекул, которые находятся в состоянии непрерывного, хаотического движения, то есть обладают кинетической энергией, а вследствие взаимодействия между собой обладают потенциальной энергией взаимодействия. Внутренняя энергия – суммарная энергия хаотического (теплового) движения микрочастиц системы и энергия взаимодействия этих частиц. Внутренняя энергия - однозначная функция термодинамического состояния системы (при переходе системы из одного состояния в другое изменение внутренней энергии определяется разностью значений внутренней энергии этих состояний и не зависит от пути перехода). Как известно из механики, движение тел (или материальных точек) происходит в пространстве и во времени. Любое движение тела можно представить как комбинацию поступательного и вращательного движений. Положение тела в каждый момент времени характеризуется числом степеней свободы. Число степеней свободы молекулы – число независимых переменных (координат), полностью определяющих положение системы в пространстве. Молекулу одноатомного газа (в виду ее малости) можно рассматривать как материальную точку, которой приписывают три степени свободы поступательного движения: i=iпост (рис. 8).
Средняя кинетическая энергия поступательного движения одноатомной молекулы идеального газа равна: E0=m0{vкв}2/2=3kT/2. Вращательные степени свободы в данном случае не учитываются, так как момент инерции данной молекулы относительно каждой из осей: Ix=mr2, Iy=mr2, Iz=mr2, расстояние до осей вращения r→0, следовательно Ix→0, Iy→0, Iz→0, тогда кинетическая энергия вращения для каждой из осей: Eк.вр.=Iω2→0. Молекула двухатомного газа рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 9). Кроме трех поступательных степеней свободы, у такой молекулы появляются две вращательные степени свободы:
i=iпост+iвращ=5 Трехатомная и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных (рис. 10):
i=iпост+iвращ=6 На самом деле, жесткой связи между атомами не существует. Атомы в молекуле могут сближаться и расходиться, то есть могут совершать колебания около положения равновесия. Энергия колебательного движения молекулы является суммой кинетической и потенциальной энергий, средние значения которых одинаковы. Таким образом, для реальных молекул необходимо учитывать также степени свободы колебательного движения. В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы – в среднем энергия, равная . Средняя энергия молекулы равна: {ε}=[i/2]·kT, (46) где i=iпост+iвращ+2iколеб Установлено, что однако энергия поступательного и вращательного движений молекулы значительно меньше энергии колебательного движения атомов в молекуле, поэтому колебательные степени свободы возбуждаются при высоких температурах. Внутренняя энергия идеального газа складывается только из кинетических энергий всех молекул в данном объеме, так как потенциальной энергией взаимодействия молекул, согласно допущениям модели идеального газа (п.1.3), можно пренебречь. Для одного моля идеального газа: Um=ENA=[i/2]·kNAT Внутренняя энергия для произвольной массы идеального газа: U=Umυ=[i/2]·mRT/M |
ВНУТРЕННЯЯ ЭНЕРГИЯ
Все тела состоят из молекул, которые непрерывно движутся и взаимодействуют друг с другом. Они обладают одновременно кинетической и потенциальной энергией. Эти энергии и составляют внутреннюю энергию тела.

Таким образом, внутренняя энергия - это энергия движения и взаимодействия частиц, из которых состоит тело. Внутренняя энергия характеризует тепловое состояние тела.
|
||||||
Первый закон термодинамики или закон сохранения энергии для тепловых процессов, связывает количество теплоты, переданное системе, изменение ее внутренней энергии и работу, совершенную системой над окружающими телами. Одна из возможных его формулировок звучит следующим образом:
Если работа совершается внешними силами над термодинамической системой, то, обозначив ее A', первый закон термодинамики можно записать в виде уравнения:
|
Билет 19
Применение первого закона термодинамики к изопроцессам.
ПРИМЕНЕНИЕ 1 ЗАКОНА ТЕРМОДИНАМИКИ К ИЗОПРОЦЕССАМ. |
|||||
Процесс |
Постоянные |
График |
Изменение внутренней энергии |
Запись 1-го закона термодинамики |
Физический смысл |
Изотермическое расширение |
m=const M=const T=const pV=const |
|
U=const U=0 |
Q=A' |
Изотермический процесс не может происходить без теплопередачи. Все количество теплоты, переданное системе, расходуется на совершение этой системой механической работы. |
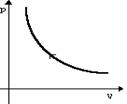
Изотермическое сжатие |
m=const M=const T=const pV=const |
|
U=const U=0 |
A=-Q |
Изотермический процесс не может происходить без теплопередачи. Вся работа внешних сил выделяется в виде тепла. |
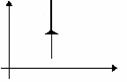
Изохорное нагревание |
m=const M=const V=const
|
p
V |
p T U U>0 |
A=0 Q= U |
Все количество теплоты, переданное системе, расходуется на увеличение ее внутренней энергии. |
Изохорное охлаждение |
m=const M=const V=const
|
p V |
p T U U<0 |
A=0 Q= U<0 |
Система уменьшает свою внутреннюю энергию, отдавая теплоокружающим телам. |
Изобарное расширение (нагревание) |
m=const M=const p=const
|
p
|
V T U U>0 |
Q=U+A' U=Q-А'>0 |
Количество теплоты, переданное системе, превышает совершенную еюмеханическую работу. Часть тепла расходуется на совершение работы, а часть – на увеличениевнутр. энергии. |
Изобарное сжатие (охлаждение) |
m=const M=const p=const
|
V |
V T U U<0 |
U=Q+A<0 Q<0 |
Количество теплоты, отдаваемое системой, превышает работу внешних сил. Часть тепла система отдает за счет уменьшениявнутр. энергии. |
Адиабатное Расширение |
m=const M=const
|
V |
U<0 U T |
Q=0 A' > 0 U=-A' < 0 A'=-U |
Система совершает механическую работу только за счет уменьшения своей внутренней энергии. |
Адиабатное сжатие |
m=const M=const
|
P V |
U>0 U T |
Q=0 A>0 U=A |
Внутренняя энергия системы увеличивается за счет работы внешних сил. |
аба́тный проце́сс термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Серьёзное исследование адиабатических процессов началось в XVIII веке.
Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна .Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы.
Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике.
Билет 20
Принцип действия тепловой машины. Коэффициент полезного действия теплового двигателя.
Большая часть двигателей на Земле - это тепловые двигатели. Устройства, превращающие энергию топлива в механическую энергию, называются тепловыми двигателями. Любой тепловой двигатель (паровые и газовые турбины, двигатели внутреннего сгорания) состоит из трех основных элементов:рабочего тела (это газ), которое совершает работу в двигателе; нагревателя, от которого рабочее тело получает энергию, часть которой затем идет на совершение работы; холодильника, которым является атмосфера или специальные устройства.
Ни один тепловой двигатель не может работать при одинаковой температуре его рабочего тела и окружающей среды. Обязательно температура нагревателя больше температуры холодильника. При совершении работы тепловыми двигателями происходит передача теплоты от более горячих тел к более холодным. Рабочее тело двигателя получает количество теплоты QН от нагревателя, совершает работу A' и передает холодильнику количество теплоты Q<subХ< sub=""></subХ<>. В соответствии с законом сохранения энергии А' < QН - QХ. В случае равенства речь идет об идеальном двигателе, в котором нет потерь энергии.
Отношение
работы к энергии, которое получило
рабочее тело от нагревателя, называют
коэффициентом полезного действия
(КПД):![]() <
1.
<
1.
В процессе работы многочисленных тепловых машин возникают тепловые потери, которые в конечном счете приводят к повышению внутренней энергии атмосферы, т. е. к повышению ее температуры. Это может привести к таянию ледников и катастрофическому повышению уровня Мирового океана, а вместе с тем к глобальному изменению природных условий. При работе тепловых установок и двигателей в атмосферу выбрасываются вредные для человека, животных и растений оксиды азота, углерода и серы. С вредными последствиями работы тепловых машин можно бороться путем повышения КПД, их регулировки и создания новых двигателей, не выбрасывающих вредные вещества с отработанными газами.

 Рис.
8. К определению числа степеней свободы
для одноатомной молекулы
Рис.
8. К определению числа степеней свободы
для одноатомной молекулы Рис.
9. К определению числа степеней свободы
для двухатомной молекулы
Рис.
9. К определению числа степеней свободы
для двухатомной молекулы Рис.
10. К определению количества степеней
свободы для трехатомной молекулы
Рис.
10. К определению количества степеней
свободы для трехатомной молекулы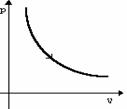

 V
V P
P P
P