Сделай модель маятника фуко сам !

Переверни табуретку вверх ножками и положи на концы её ножек (по диагонали) какую-нибудь рейку. А к середине её подвесь небольшой груз (например, гайку)ни нити. Заставь его качаться так, чтобы плоскость качания проходила между ножек табуретки. Теперь медленно поворачивай табуретку вокруг её вертикальной оси. Тебе станет заметно, что маятник качается уже в другом направлении. На самом деле он качается всётакже, а изменение произошло из-за поворота самой табуретки, которая в этом опыте играет роль Земли.

Крутильный маятник

Это маятник Максвелла, он позволяет выявить ряд интересных закономерностей движения твердого тела. К диску, насаженному на ось, привязаны нити. Если закрутить нить вокруг оси, диск поднимется. Теперь отпускаеммаятник, и он начинает совершать периодическое движение: диск опускается, нить раскручивается. Дойдя до нижней точки, по инерции диск продолжает вращаться, но теперь уже закручивает нить и поднимается вверх.

___

Обычно крутильный маятник применяется в механических наручных часах. Колесико-балансир под действием пружины вращается то в одну, то в другую сторону. Его равномерные движения обеспечивают точность хода часов.

Сделай крутильный маятник сам!

Вырежьте из плотного картона небольшой круг диаметром 6 – 8 см. На одной стороне кружка нарисуйте открытую тетрадь, а на другой стороне – цифру «5». С двух сторон круга проделайте иголкой 4 отверстия и вставьте 2 прочные нити. Закрепите их, чтобы они не выскакивали, узелками. Далее стоит лишь закрутить круг на 20 – 30 оборотов и натянуть нити в стороны. В результате вращения вы увидите картинку « 5 в моей тетрадке».  Приятно?

Знаешь ли ты ?

Ртутное «сердце» тоже колеблется!  Небольшая капля – лужица ртути, поверхности которой в её центре касается железная проволока – игла, залита слабым водяным раствором соляной кислоты, в котором растворена соль двухромовокислого калия.. Ртуть в растворе соляной кислоты получает электрический заряд и поверхностное натяжение на границе соприкасающихся поверхностей понижается. При соприкосновении иглы с поверхностью ртути заряд уменьшается и, следовательно, меняется поверхностное натяжение. При этом капля обретает более сферическую форму. Макушка капли наползает на иглу, а затем под действием силы тяжести соскакивает с неё. Внешне это явление производит впечатление вздрагивания капли ртути. Этот первый импульс дает толчок колебаниям, капля раскачивается и «сердце» начинает пульсировать. Ртутное «сердце» - не вечный двигатель! Со временем длина иглы уменьшается, и её вновь приходится устанавливать в соприкосновение с поверхностью ртути.

Источник: ж. «Квант»

___

В аэродинамике известно явление, называемое флаттером, - самопроизвольные колебания крыла в полете, приводящее к его поломке и аварии. Для гашения вредных колебаний переднюю кромку каждого крыла стали утяжелять. Природа также выработала средство борьбы с флаттером. У стрекоз, например, на каждом крыле, в вершинной его части, у переднего края имеется темное хитиновое утолщение.

Основные характеристики колебательного движения. 1. Период - время одного полного колебания. За период тело проходит расстояние, равное 4-м амплитудам 2. Линейная частота – число колебаний за 1 секунду. Герц. – период и линейная частота взаимообратные величины. Математический маятник с короткой нитью имеет большую линейную частоту колебаний, чем математический маятник с длинной нитью. “Т” и “ ” для данной колебательной системы – характерные только для данной системы величин. 3. Циклическая или круговая частота – число колебаний за 2? секунд. 4. Х [м] – смещение точки от положения равновесия в данный момент времени. 5. А=Хmax [м] – амплитуда – модуль максимального смещения тела от положения равновесия. 6. Фаза – физическая величина, описывающая состояние колебательной системы в данный момент времени. – величина, стоящая под знаком синуса или косинуса. 11.

Слайд 16 из презентации «Урок механические колебания» к урокам физики на тему «Колебания»

Размеры: 720 х 540 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке физики, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как...». Для показа на уроках Вы также можете скачать всю презентацию «Урок механические колебания.ppt» бесплатно в zip-архиве. Размер архива - 375 КБ.

СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

При совпадении частоты вынужденных колебаний с частотой свободных колебаний системы наступает резонанс. Гармонические свободные и вынужденные колебания характеризуют амплитудой, периодом и фазой.   

Многие процессы вокруг нас повторяются во времени. Так, звук электрического звонка представляет собой периодически повторяющиеся изменения давления воздуха. При этом ток в электрической цепи звонка тоже периодически изменяется или, как говорят, является переменным. Периодические изменения любых физических величин называют колебаниями.

Примером колебаний могут служить колебания положения груза, подвешенного на пружине. Если вывести груз из положения равновесия, оттянув его вниз и отпустить, то груз начнёт совершать колебательные движения – вверх-вниз, вверх-вниз и т.д. Если пренебречь силой трения о воздух, действующей на груз, то систему «пружина-груз-Земля» или пружинный маятник можно считать замкнутой. Колебания физических величин, возникающие в замкнутых системах под действием внутренних сил, называют свободными колебаниями.

Рассмотрим причины возникновения свободных колебаний на примере пружинного маятника. При отклонении груза вниз на расстояние А от положения равновесия сила упругости пружины возрастает, и когда груз отпускают (рис. 8а), он начинает двигаться с ускорением вверх к положению равновесия и скорость его растёт. Через некоторое время груз достигает положения равновесия и в этот момент сумма сил, действующих на груз, становится равной нулю, а скорость его – максимальной v_max (рис. 8б). Затем груз по инерции проходит положение равновесия и отклоняется в противоположную сторону, в результате чего пружина укорачивается, и результирующая сил, приложенных к грузу, начинает действовать вниз, тормозя его движение. В самом верхнем положении скорость груза уменьшается до нуля (рис. 8в), а потом под действием результирующей силы он опять начинает двигаться к положению равновесия, увеличивая свою скорость. Но при достижении точки равновесия груз приобретает максимальную скорость и опять проскакивает точку равновесия (рис. 8г). Потом груз постепенно тормозится до полной остановки в крайнем нижнем положении (рис. 8а), и всё повторяется сначала.  

Сила, стремящаяся возвратить систему в положение равновесия, является необходимым условием появления свободных колебаний в пружинном маятнике и других колебательных системах. Отметим, что в крайних положениях пружинного маятника (рис. 8а,в) система обладает только потенциальной энергией деформированной пружины. Наоборот, когда груз проходит через положение равновесия (рис. 8б,г), система обладает только кинетической энергией.

Колебания, вызванные внешними периодически изменяющимися силами, называют вынужденными колебаниями. Например, можно вызвать вынужденные колебания у обычных подвесных качелей, если периодически толкать их в разные стороны. Из опыта известно, что вынужденные колебания достигают наибольшей амплитуды, когда их частота совпадает с частотой свободных колебаний системы. Такое резкое возрастание амплитуды вынужденных колебаний называют резонансом.

Периодические изменения физических величин, происходящие по закону синуса или косинуса, называются гармоническими колебаниями. Так, например, изменения положения x и вертикальной скорости v пружинного маятника со временем t можно описать следующим образом (см. рис 8д):

x=-A^.cos(t)                                          (8.1)

v=v_max^.sin(t),                                        (8.2)

где A и v_max^. – амплитуды соответствующих колебаний, а   - их циклическая или круговая частота, которая следующим образом связана с обычной частотой  и периодом колебаний Т:

    

Величину, от которой берут синус или косинус в (8.1-2), называют фазой колебаний, . Как следует из (8.1-2), фаза колебаний определяет состояние системы.

Вопросы для повторения:

        Что называют свободными и вынужденными колебаниями системы?

        Какие колебания называют гармоническими?

        Как связаны между собой круговая частота, период и фаза колебаний?

 

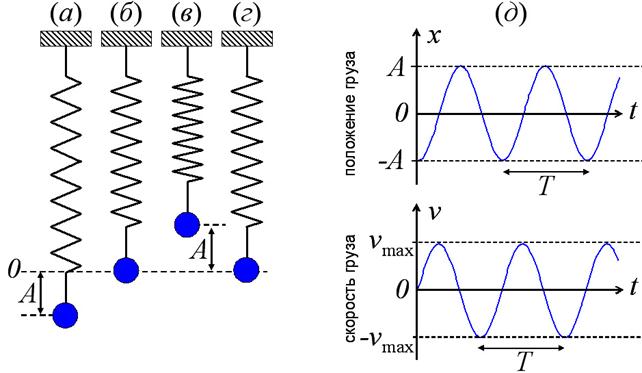Рис. 8. Положения пружинного маятника в различные моменты (а-г) его колебаний и графики зависимости изменений положения груза x и его вертикальной скорости v от времени t (д).

Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;   — полная фаза колебаний,   — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической часто

Билет 51

Электромагнитными колебаниями называются периодические изменения напряженности Е и индукции В.

Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.

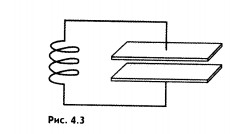
Простейшая система, в которой могут происходить свободные электромагнитные колебания, состоит из конденсатора и катушки, присоединенной к его обкладкам (рис. 4.3), и называется колебательным контуром.

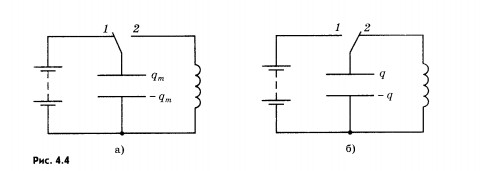
Зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя (рис. 4.4, а). При этом конденсатор получит энергию   где q_m — заряд конденсатора, а С — его электроемкость. Между обкладками конденсатора возникнет разность потенциалов U_m. Переведем переключатель в положение 2 (рис. 4.4, б). Конденсатор начнет разряжаться, и в цепи появится электрический ток. Сила тока не сразу достигает максимального значения, а увеличивается постепенно. Это связано с явлением самоиндукции.  ЭДС самоиндукции возникает при появлении тока в цепи и препятствует его увеличению, поэтому ток в цепи растет постепенно.

По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока, которая определяется формулой где i — сила переменного тока; L — индуктивность катушки.

Полная энергия W электромагнитного поля контура равна сумме энергий его магнитного и электрического полей:     В момент, когда конденсатор полностью разрядится (q = 0), энергия электрического поля станет равной нулю. Энергия же магнитного поля тока, согласно закону сохранения энергии, будет максимальной. В этот момент сила тока также достигнет, конечно, максимального значения I_m.

Несмотря на то что к этому моменту разность потенциалов на концах катушки становится равной нулю, электрический ток не может прекратиться сразу. Этому препятствует явление самоиндукции. Как только сила тока и созданное им магнитное поле начнут уменьшаться, возникает ЭДС самоиндукции, стремящаяся поддержать ток.

В результате конденсатор будет перезаряжаться до тех пор, пока сила тока, постепенно уменьшаясь, не станет равной нулю. Энергия магнитного поля в этот момент также будет равна нулю, энергия электрического поля конденсатора опять станет максимальной.

После этого конденсатор вновь начнет перезаряжаться, и система возвратится в исходное состояние. Если бы не было потерь энергии, то этот процесс продолжался бы сколь угодно долго. Колебания были бы незатухающими. Через промежутки времени, равные периоду колебаний, состояние системы в точности повторялось бы. Полная энергия при этом сохранялась бы неизменной, и ее значение в любой момент времени было бы равно максимальной энергии электрического поля или максимальной энергии магнитного поля:   Но в действительности потери энергии неизбежны. Так, в частности, катушка и соединительные провода обладают сопротивлением R, а это ведет к постепенному превращению энергии электромагнитного поля во внутреннюю энергию проводника.

В колебательном контуре энергия электрического поля заряженного конденсатора периодически переходит в энергию магнитного поля тока. При отсутствии сопротивления в контуре полная энергия электромагнитного поля остается неизменной.

Билет 52

Вынужденные Электромагнитные Колебания

Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.

Принцип действия генератора переменного тока легко показать при рассмотрении вращающейся рамки провода в магнитном поле.

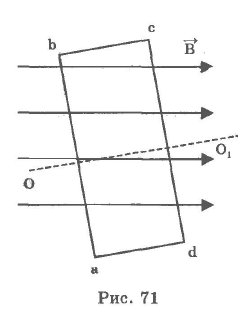
В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).

Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.

Магнитный поток в момент времени t₀ = 0 будет равен Ф = В*8.

При равномерном вращении рамки вокруг оси OO₁ с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:

Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную

где Е₀= ВSw - амплитуда ЭДС.

Если с помощью контактных колец и скользящих по ним щеток соединить концы рамки с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания силы тока - переменный ток.

На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора - неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец. 

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

Билет 53